Two charges of # -5 C # and # -1 C# are positioned on a line at points # 3 # and # 5 #, respectively. What is the net force on a charge of # 2 C# at # -2 #?

Question

1327 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-03-25T21:08:29

#"Net Force is " -3.97*10^9 units#
#"The negative sign shows that charges at the points A and B "##"attract the charge at the point of C."#

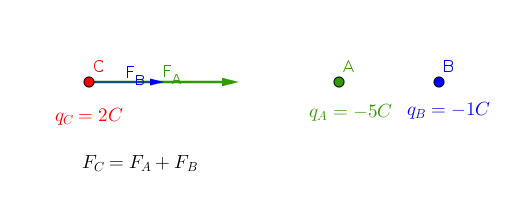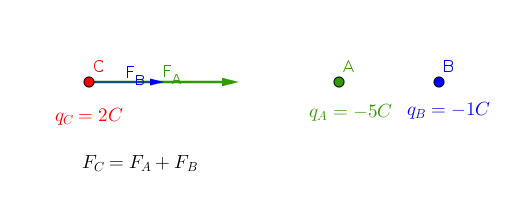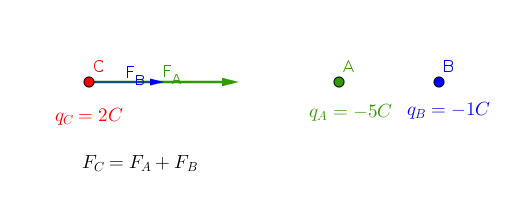
enter image source here

#"Both of charge at the points A and B apply a force on"#
#"the charge at the point of C."#

#"let "F_A" be a force that A applies C." #

#"The charge at the point of A attracts the charge at C"#

#color(green)(F_A)=(k*q_A*q_C)/(d_("AC")^2)=-(K*5*2)/(3+2)^2=-(K*2.5)/25=-(2K)/5#

#"let "F_B" be a force that B applies C." #

#"The charge at the point of B attracts the charge at C"#

#color(blue)(F_B)=(k*q_B*q_C)/(d_("BC")^2)=-(K*1*2)/(5+2)^2=-(K*2.1)/49=-(2K)/49#

#color(red)(F_C)=color(green)(F_A)+color(blue)(F_B)#

#color(red)(F_C)=-(2K)/5 -(2K)/49#

#color(red)(F_C)=-2K(1/5+1/49)#

#color(red)(F_C)=-2K((49+5)/(49*5))#

#color(red)(F_C)=-2K(54)/(245)#

#K=9*10^9#

#color(red)(F_C)=-2*9*10^9(54/245)#

#color(red)(F_C)=-3.97.10^9 "#