Two particles A and B of equal mass M are moving with the same speed v as shown in the figure. They collide completely inelastically and move as a single particle C. The angle θ that the path of C makes with the X-axis is given by :?
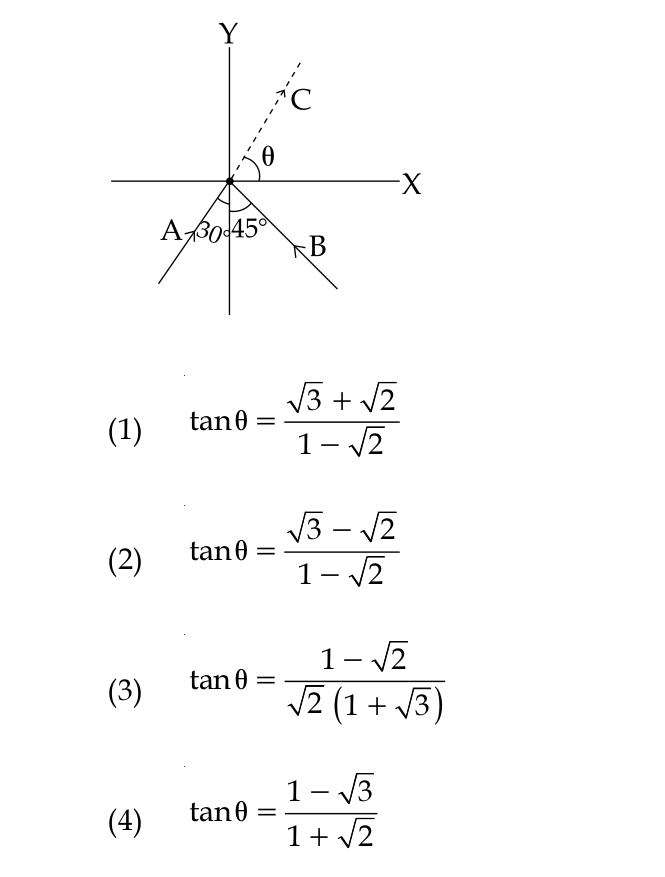
1 Answer
Explanation:
In physics, momentum must always be conserved in a collision. Therefore, the easiest way to approach this problem is by splitting up each particle’s momentum into its component vertical and horizontal momentums.
Because the particles have the same mass and velocity, they must also have the same momentum. To make our calculations easier, I will just assume that this momentum is 1 Nm.
Starting with particle A, we can take the sine and the cosine of 30 to find that it has a horizontal momentum of
For particle B, we can repeat the same process to find that the horizontal component is
Now we can add together the horizontal components to get that the horizontal momentum of particle C will be
Once we have these two component forces, we can finally solve for

