Two rays of light are incident normally on a tub of height #H# filled with water. They pass through glass slabs of heights #h_1# and #h_2#. If the speed of light in vacuum is #c#, what is the time difference between the rays of light to reach the bottom?
Refractive indices of water and glass are #4/3# and #3/2# respectively.
Refractive indices of water and glass are
1 Answer
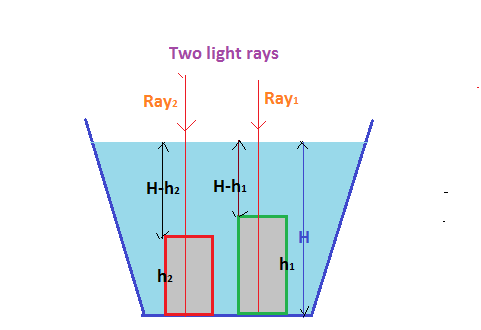
The situation described in the problem is shown in the above figure
As the rays of light are incident normally , the rays will refracted through the media without deviation.
For slab of height
the total path length of water and glass =H
Path length of glass medium
Then path length of water medium
For slab of height
the total path length of water and glass =H
Path length of glass medium
Then path length of water medium
We know refractive index of water
Again we know refractive index of glass
Calculation of time to reach
So time taken by the light
And time taken by the light
Hence total time
Calculation of time to reach
Now time taken by the light
And time taken by the light
Hence total time
Hence the time difference between the two rays of light to reach the bottom is given by

