Two vectors with lengths 1.00 m and 2.00 m have an angle of 30.0° between them .What is the square of the length of the resultant vector?

Question

2745 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-03-04T19:10:44

#= 5 - 2 sqrt 3#

#approx 1.56#

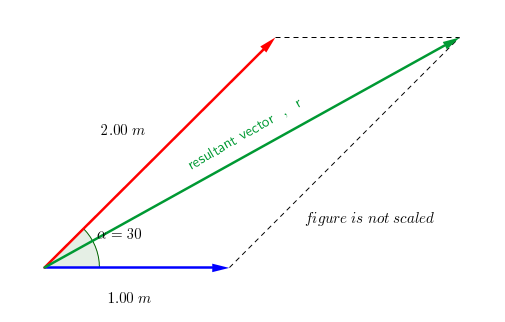
For vectors # mathbf a, mathbf b#, the length of the resultant vector, #mathbf c = mathbf a - mathbf b#, is:

#abs ( mathbf c ) = sqrt( (mathbf a - mathbf b) cdot (mathbf a - mathbf b))#

And:
#abs ( mathbf c )^2 = (mathbf a - mathbf b) cdot (mathbf a - mathbf b)#

#= mathbf a cdot mathbf a + mathbf b cdot mathbf b - 2 mathbf a cdot mathbf b #

And because:

#mathbf a cdot mathbf b = abs( mathbf a) abs( mathbf b) cos alpha#
#mathbf v cdot mathbf v = abs( mathbf v) abs( mathbf v) cos 0= |mathbf v|^2#

We have:

#= 1^2 + 2^2 - 2 (1)(2) cos (pi/6) #

#= 5 - 2 sqrt 3#

#approx 1.56#

Answer 2 · 2017-03-04T19:31:23

#"the square of the length of the resultant vector is "l^2=6.73#

enter image source here

#"let the resultant vector be "vec r#

#"let length of " vec r" be l"#

#l^2=(1.00)^2+(2.00)^2+2*1.00*2.00*cos 30#

#cos 30=0.8660254#

#l^2=1+4+2*0.8660254#

#l^2=5+1.7320508#

#l^2=6.7320508#

#l^2=6.73#