Question

Use a sine function to describe the height of the tides of the ocean if high tide raises the water level to 5 metres at noon and low tide drops it down to 1 metre at 4 p.m. Let t=0 be 12 noon?

Answer 1

`h(t)=2sin(pi/2-1/12pit)+3`

Explanation:

Given at `t=0`, max height =5m
And `t=4` ,min height =1
Since it is a complete day period(P)=24
We know average =`1/2` [Max+Minimum]
`=1/2 (5+1)`
`=1/2×6`
`=3`

Again,
Amplitude(A) is the maximum displacement from average hence
#A=abs (5-3) :.A=2#

Firstly let's start with a cosine wave since at t=0 it is at maximum.

`h (x)=Acos (Bx)+` Average
Since period is 24.So the coefficient of B as per the formula,`P=2pi/B`
`24=2pi/B`
`or, B=2pi/24`
`:.B=pi/12`
Hence,
`h (t)=2cos (pi/12t)+3`
Again by co-function identity `cos (x)=(pi/2-x)`
Substitute,
`h(t)=2sin(pi/2-pi/12t)+3` is the required model

Answer 2

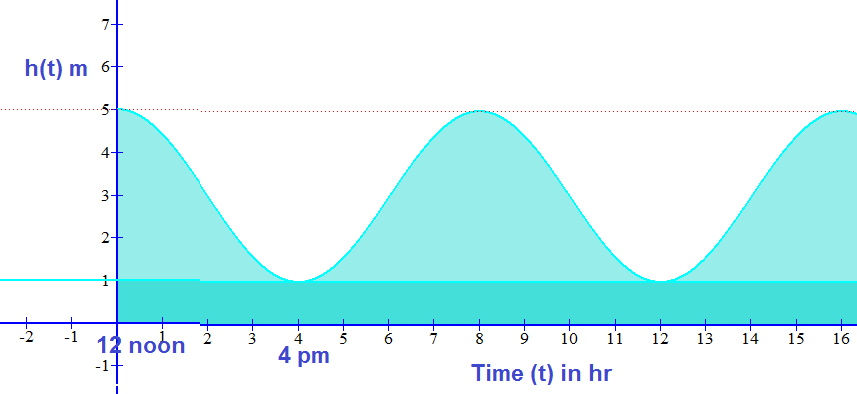
Given that high tide raises the water level to 5 metres at noon and low tide drops it down to 1 metre at 4 p.m. The height of water level varies from 1m to 5m. So Rise and fall of height of water level is 2m across the equilibrium height of 3m. So amplitude of periodic movement of water level is `A=2m`

The half cycle of tide from high tide to low tide requires time 12noon to 4pm i.e. 4 hrs. So time period of this periodic movement of water level will be `T=8hrs`. Hence angular velocity associated with this periodic movement of water level is `omega=(2pi)/8=pi/4`

The cosine function which describes this periodic variation of height of water will be given by

`h(t)=3+Acos(omegat)`

`=>h(t)=3+2cos((pit)/4)`

Converting this into sine function as desired ,we get

`h(t)=3+2sin(pi/2-(pit)/4)`

`=>h(t)=3-2sin((pit)/4-pi/2)`