Use Newton's method to find the coordinates of the inflection point of the curve?
#y=e^cosx# 0 ≤ x ≤ π , correct to six decimal places.
1 Answer
Explanation:
First let us look at the graph
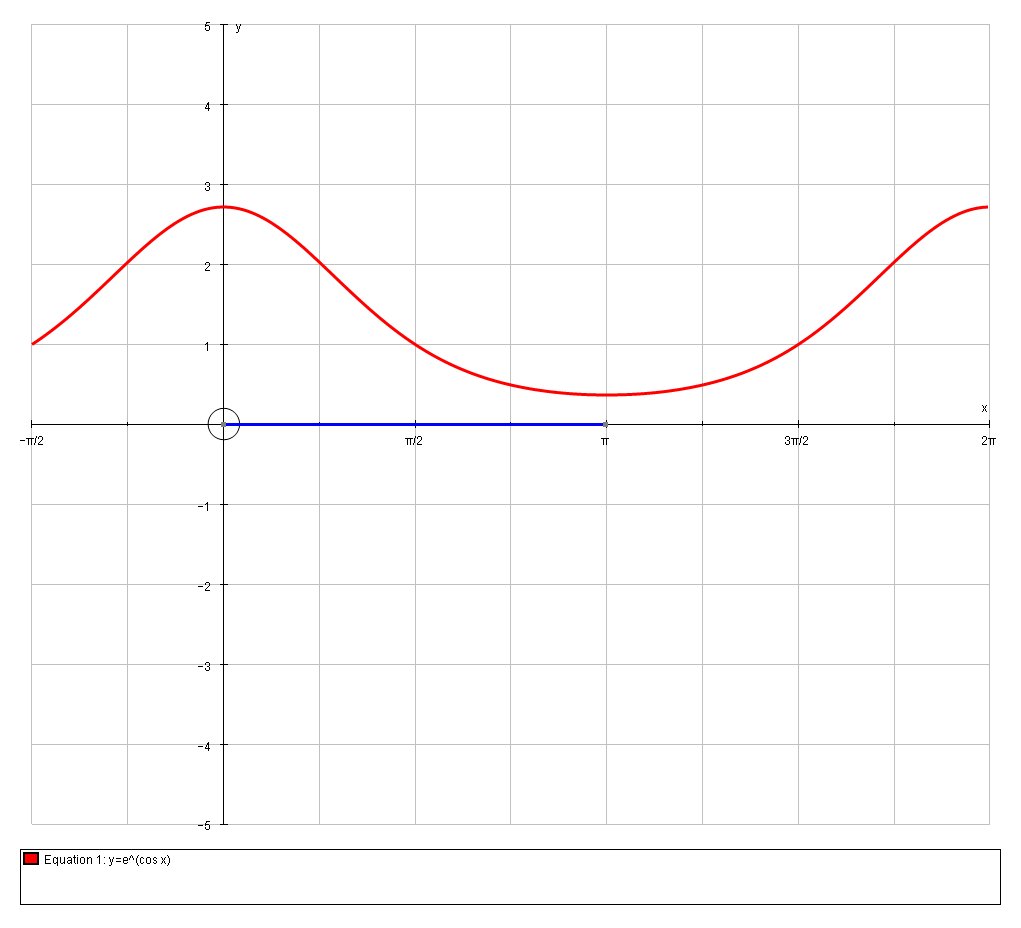
Inflection points are the points of the curve where the curvature changes its sign, and from the graph I would predict there is one point
A necessary condition for an inflection point is that
So if:
# f(x) = e^(cosx) #
Then using the chain rule we have
# f'(x) = e^(cosx)*(-sinx) #
#" "= -sinx e^(cosx) #
And as we need the second derivative we differentiate again (using the product rule) to get:
# f''(x) = (-sinx)(-sinx e^(cosx)) + (-cosx)(e^(cosx)) #
#" "= sin^2x \ e^(cosx) -cosx \ e^(cosx) #
#" "= (sin^2x -cosx ) e^(cosx) #
Our necessary condition is
# (sin^2x -cos x) e^(cosx) =0 #
And as
# sin^2x -cos x =0 #
So our aim is to solve the equation
We therefore need
# \ \ g(x) = (sin^2x -cosx ) e^(cosx) #
#g'(x)= (sin^2x -cosx)(-sinx e^(cosx)) + (2sinxcosx-sinx)(e^(cosx)) #
# " " = -sinx \ e^(cosx)( sin^2x -cosx -2cosx-1) #
# " " = -sinx \ e^(cosx)( sin^2x -3cosx-1) #
Then using excel working to 8dp we can tabulate the iterations as follows:

We have confirmed our necessary condition for an inflection point but we need to establish the necessary condition: that is
And using a calculator we can easily verify that with
#f''(x)~~0# ,#f''(x-epsilon) <0# and#f''(x+epsilon) >0#
And we conclude that the solution is#x=0.904557# to 6dp
Hence
Exact Solution
NB: We can solve our equation for an exact answer
# (1-cos^2x) -cos x =0 #
# :. cos^2x +cos x -1 =0 #
This is a quadratic in
# (cos x+1/2)^2 -(1/2)^2-1 =0 #
# :. (cos x+1/2)^2 =5/4 #
# :. cos x+1/2 =+-1/2sqrt(5) #
# :. cos x =1/2(sqrt(5)-1) " " (because 0 le x le pi)#
# :. cos x =0.61803... #
# :. x =0.90455... #
Bear this in mind when problem solving as N-R was actually harder than solving the equation directly

