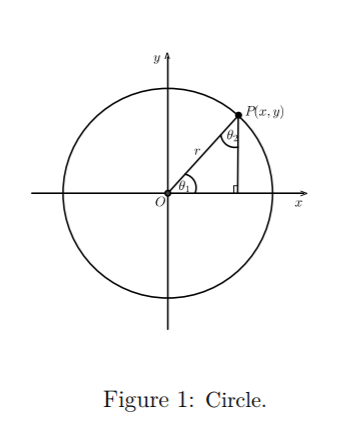
general equation of circle: #x^2+y^2 = r^2#
#x^2 + y^2# is the square of the radius of the circle made by the graph.
here, #r=1#.
#r^2 = 1^2 = 1#.
if #theta_1 = theta_2#, then the triangle is isosceles.
this means that the horizontal and vertical sides of the triangle are equal.
these two sides are the horizontal and vertical components of point P. they are equal, meaning that the #x#- and #y#- values of P are equal.
#x^2 + y^2 = 1#
#x = y#
#y# can be substituted for #x# (or vice versa) to find the values of both.
#x^2 + x^2 = 1#
#2x^2 = 1#
#x^2 = 1/2#
#x = sqrt(1/2)#
#sqrt(x/y) = (sqrtx)/(sqrty)#
#sqrt(1/2) = (sqrt1)/(sqrt2)#
#=1/sqrt2#
#x = 1/sqrt2, y = 1/sqrt2#
#cos theta_1# is the side adjacent to #theta_1# over the hypotenuse.
the side adjacent to #theta_1# is the horizontal, so the length of the adjacent is equal to the value of #x# at point P.
the hypotenuse is the radius of the circle, which is #1#.
#cos theta_1 = A/H = x/1#
#cos theta_1 = (1/sqrt2)/1 = 1/sqrt2#
#sin theta_2# is the side opposite to #theta_1# over the hypotenuse.
the side opposite to #theta_1# is the same side as is adjacent to #theta_2#. its length is the value of #x# at point P.
#O /H = x/1 #
#= 1/sqrt2#
#sin theta_2 = 1/sqrt2#