Use the graph to determine each local extrema? (See Image)
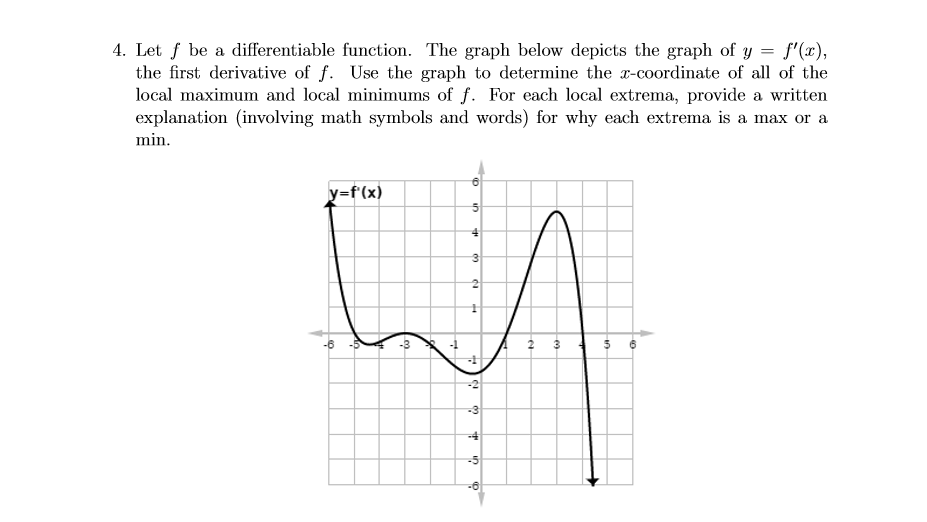
1 Answer
Apr 29, 2017
Local maxima:
Local minima:
Explanation:
A graph
This is because
Note:

Local maxima:
Local minima:
A graph
This is because
Note: