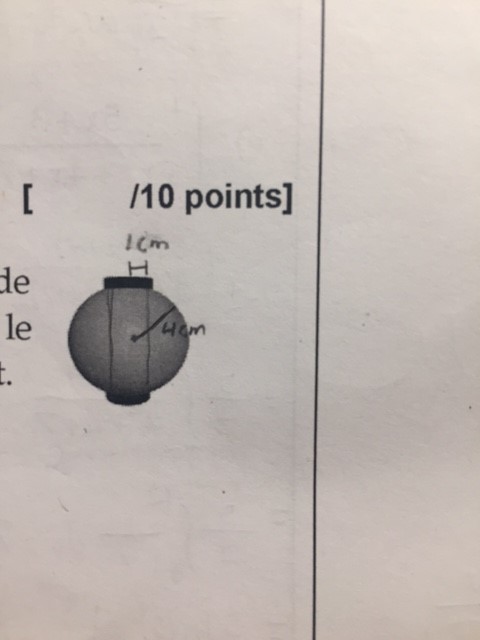
Using a crankshaft, a carpenter drills a hole ,1 cm in radius, through a wooden ball along a diameter. If the radius of the ball is 4 cm, what is the volume of wood remaining? .
1 Answer
Calculate the removed portion and subtract it from the original volume.
Explanation:
The removed portion is a cylinder with two spherical portion caps. A quick approximation could be done by ignoring the curvature. In that case the cylinder volume is just:
The Sphere volume is
The remaining volume (approximated) is thus
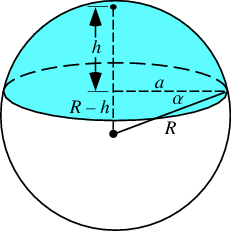
To find the exact volume removed, add the volume of the caps:
h = 0.127 (calculated from chord "a" - cut radius of 1 - see graphic)
We have to take TWO of those for a total volume of 0.401
The revised cylinder length is 4 - 0.254 = 3.746
Add this to the caps:
The remaining volume (exact) is thus