Question

Using Hess' Law, how do you calculate the standard heat of formation of Copper(I) Oxide given the following data?

`CuO(s) -> Cu(s)+ 1/2 O_2` `Delta H = 157.3 kJ` `/` `mol`
`4CuO(s) -> 2Cu_2O(s) + O_2(g)` `Delta H 292.0 kJ` `/` `mol`

Answer 1

You can do it like this:

Explanation:

Hess' Law states that the overall enthalpy change of a process is independent of the route taken.

In thermodynamics we are interested in initial and final states.

You need to construct a Hess Cycle using the information given:

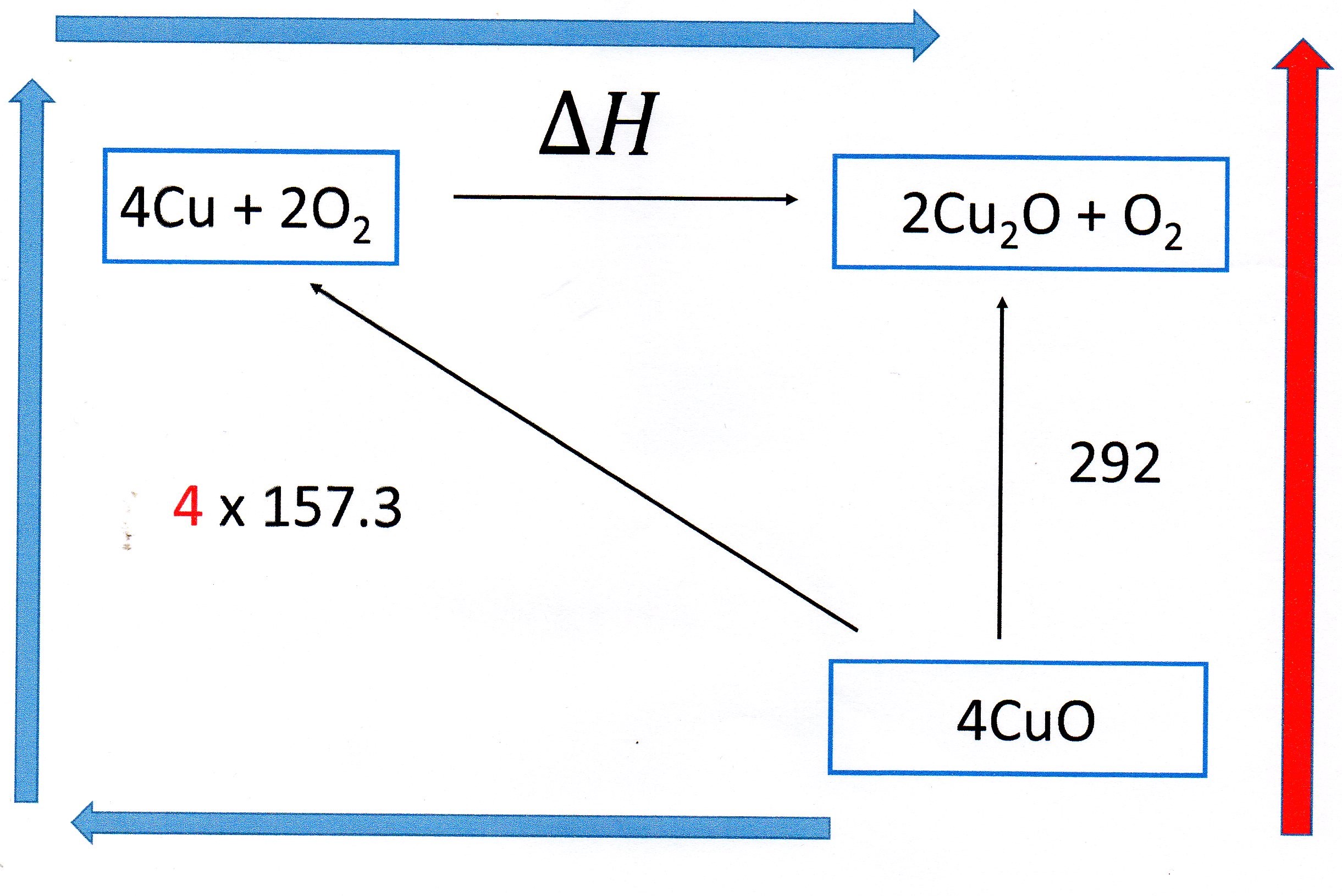
You can see that, in energy terms, the `color(blue)("blue")` route is equal to the `color(red)("red")` route as the arrows start and finish in the same place. This is in accordance with Hess' Law.

So we can write:

`(4xx157.3)+DeltaH=292`

`:.DeltaH=-337.2"kJ"`

Enthalpy of formation refers to the formation of 1 mole of a substance from its elements in their standard states under standard conditions.

We have found `DeltaH` for:

`4Cu+2O_2rarr2Cu_2O +O_2`

Which is the same as:

`4Cu+O_2rarr2Cu_2O`

This refers to the formation of 2 moles of copper(I) oxide. We need the enthalpy change for the formation of 1 mole of copper(I) oxide.

`:.DeltaH_f[Cu_2O]=(DeltaH)/2=-337.2/2=-168.6"kJ/mol"`