Using Polar coordinates, what is the area of region A?

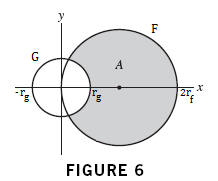
enter image source here

F: #r# = 16 #cos(Theta)#
#r_f# = 8

G: #r# = 5
#r_g# = 5

1 Answer
A. S. Adikesavan
Jul 10, 2018

# ( (5/2)sqrt 231 + 103 cos^(-1)(5/16) )#
#= ( 5/2 sqrt 231 + 129.056 rad)#= 167.05 areal units, nearly.
This is nearly 83.1 % of the area of the larger circle.

Explanation:

At the common points,

#r = 16 cos theta = 5#, giving #cos theta = 5/16# and

#(5, +-cos^(-1)(5/16))#, as the points of intersection.

So, the shaded area

#= 2 int [int r dr] d theta#,

between the limits 5 and #16 costheta#, for r,

and 0 and #cos^(-1)(5/16)#, for #theta#

#= int (16^2cos^2theta - 5^2) d theta#,

#theta# from 0 to #cos^(-1) (5/16)#

#= int (256 cos^2theta -25) d theta, theta# from 0 to #cos^(-1)

(5/16)#

#= int ( 128 cos 2theta + 103 )] d theta #, between the limits

#=[ 64 sin 2theta + 103 theta ]#, between the limits

#=( 128( sqrt( 1-(5/16)^2)(5/16)) + 103 cos(-1)(5/16))#

# = ( (5/2)sqrt 231 + 103cos(-1)(5/16) )#

#= ( 5/2 sqrt 231 + 129.056 rad)#

#= 167.05 areal units, nearly.

Related questions
Impact of this question
1576 views around the world
You can reuse this answer
Creative Commons License