Using standard electrode potentials in a consistent manner?
Given the following values, which reaction is spontaneous?
#Cu^(2+)+2e^(-)->Cu # 0.34 V
#Zn^(2+) + 2e^(-) -> Zn# -0.76 V
#Ag^(+) + e^(-) -> Ag# 0.8 V
A. #2Ag + Zn^(2+) -> Zn + 2Ag^(+)#
B. #Cu^(2+) + Zn -> Zn^(2+) + Cu#
C. #Cu^(2+) + 2Ag -> 2Ag^(+) + Cu#
D. #Zn^(2+) +Cu -> Cu^(2+)+ Zn#
Now, my question is rather what method to use to solve this question. In my book they refer to use the Formula:
E(cell) = E(cell were reduction occurs)- E(cell were oxidation occurs). However, using this in the first example we get:
(-0.76)- (-0.8)=0.04, which is wrong as Silver will not oxidize spontaneously. Though this works if one does not change the sign on the oxidation:
(-0.76)-(0.8)=-1.56, which is correct. However, then we have not switched signs to account for the oxidation reaction, but is that what one should do?
Similarly, my teacher told me to :
"Take the highest value and subtract the lowest value". Then we get:
(-0.76)-(-0.8)=0.04, again, wrong.
Or (0.8)-(-0.76)=1.56, which is also wrong!
So my question is, how does one determine the standard electrode potential consistently? If you have a formula/strategy on how to tackle these problems in a consistent way I would be very happy to hear it!
Given the following values, which reaction is spontaneous?
A.
B.
C.
D.
Now, my question is rather what method to use to solve this question. In my book they refer to use the Formula:
E(cell) = E(cell were reduction occurs)- E(cell were oxidation occurs). However, using this in the first example we get:
(-0.76)- (-0.8)=0.04, which is wrong as Silver will not oxidize spontaneously. Though this works if one does not change the sign on the oxidation:
(-0.76)-(0.8)=-1.56, which is correct. However, then we have not switched signs to account for the oxidation reaction, but is that what one should do?
Similarly, my teacher told me to :
"Take the highest value and subtract the lowest value". Then we get:
(-0.76)-(-0.8)=0.04, again, wrong.
Or (0.8)-(-0.76)=1.56, which is also wrong!
So my question is, how does one determine the standard electrode potential consistently? If you have a formula/strategy on how to tackle these problems in a consistent way I would be very happy to hear it!
2 Answers
B. Because it has a positive voltage or electric potential
Explanation:
Well here is what I do...
You know that in a reaction both species can't be reduced, 1 species always has to be oxidized and one always has to be reduced. In your table, all the reduction eV are stated, so you are going to have to change the sign on one of them, so they can be oxidized.
- When looking at the first reaction, 2Ag is being oxidized, so not only will you change the sign but also multiply the value by 2. -1.6eV, Zn+2 is being reduced, so just use the formula table value, -1.6+-.76= -2.36 eV, so this is definitely not spontaneous
This is how I approach each one of those.
Many students use the anticlockwise rule to determine whether a redox reaction will occur between two species.
Explanation:
The rule is easier to demonstrate than to define.
A.
Will metallic
Solution
Step 1. Write the standard reduction half-reactions for
Step 2. Use the anticlockwise rule.
Draw arrows (the red arrows in the diagram below) anticlockwise above and below your equations.
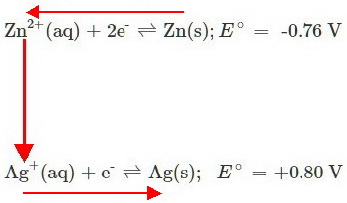
The diagram tells us that
- Electrons will flow from the
#"Zn"# equilibrium to the#"Cu"# one (the vertical arrow) - The position of the
#"Zn"# equilibrium moves to replace the electrons being lost (the top arrow) - The position of the
#"Ag"# equilibrium moves to remove the extra electrons (the bottom arrow)
The
Step 3. Determine the equation for the reaction that will occur
We must reverse the top equation.
The rule predicts that
The other conclusion is that


