Question

Using the chemical equation below, determine the energy released by burning 2 moles of propane, `"C"_3"H"_8`? a) 4438.4 kJ b) 11096 kJ c) 2219.2 kJ d) 1109.6 kJ

`"C"_3"H"_8(g) + 5"O"_2(g) → 3"CO"_2(g) + 4"H"_2"O"(l) + "2219.2 kJ"`

Answer 1

`DeltaH ^o"_(rxn)` 2 moles of Propane gas = -3295 Kj => None of the listed energy values are for combustion of 2 moles Propane.

Explanation:

Using values from Thermodynamic Properties table and applying to the Hess's Law Equation, the following was obtained ...

Answer 2

`"4438.4 kJ"`

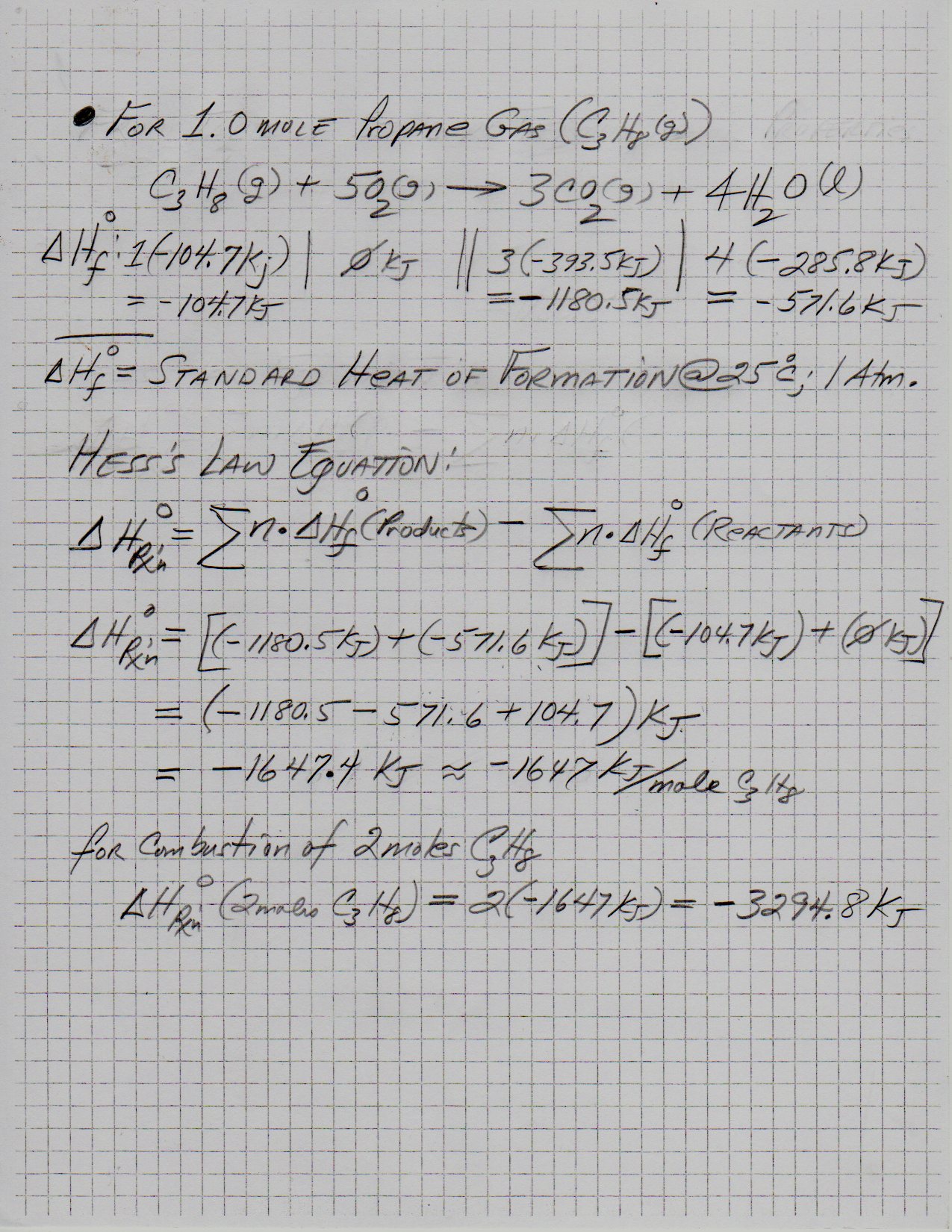
Explanation:

The problem provides you with the thermochemical equation that describes the combustion of propane.

`"C"_ 3"H"_ (8(g)) + 5"O"_ (2(g)) -> 3"CO"_ (2(g)) + 4"H"_ 2"O"_ ((l)) + color(blue)("2219.2 kJ")`

This tells you that when `1` mole of propane undergoes combustion, `color(blue)("2219.2 kJ")` of heat are being given off.

In your case, you want to know how much heat will be given off when `2` moles of propane undergo combustion. You can use the aforementioned ratio as a conversion factor to get

`2 color(red)(cancel(color(black)("moles C"_3"H"_8))) * overbrace("2219.2 kJ"/(1color(red)(cancel(color(black)("mole C"_3"H"_8)))))^(color(red)("given by the balanced thermochemical equation")) = color(darkgreen)(ul(color(black)("4438.4 kJ")))`

Alternatively, you can multiply all the products and all the reactants, including the heat given off by the reaction, by `color(red)(2)`

`color(red)(2)"C"_ 3"H"_ (8(g)) + (color(red)(2) * 5)"O"_ (2(g)) -> (color(red)(2) * 3)"CO"_ (2(g)) + (color(red)(2) * 4)"H"_ 2"O"_ ((l)) + (color(red)(2) * color(blue)("2219.2 kJ"))`

to get

`2"C"_ 3"H"_ (8(g)) + 10"O"_ (2(g)) -> 6"CO"_ (2(g)) + 8"H"_ 2"O"_ ((l)) + color(darkgreen)(ul(color(black)("4438.4 kJ")))`

Once again, you can say that when `2` moles of propane undergo combustion, `"4438.4 kJ"` of heat are being given off.