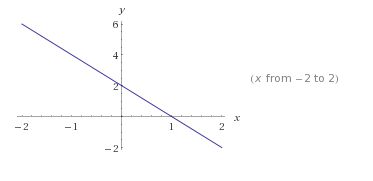
Looking at the graph of #y = 2 - 2x#, imagine the area between the line, the x-axis, and the y-axis, being revolved around the x-axis. You'll end up with a cone, with the point/tip at #x = 1#, and the center of the circular base (which has radius 2) at the origin.
Next, imagine looking at a cross-section parallel to the x-z axis - parallel to the circular base. Every cross-section will be a circle. At #x = 0#, the circle has radius 2, and at #x = 1#, the circle has radius 0. In fact, for any #x#, the cross-sectional circle has radius #2 - 2x#.
To find the volume of the solid of revolution, we can imagine that our solid is composed of infinitely many disks, of infinitesimal width, and radius equal to #2 - 2x#. To find the volume of the solid, we sum up (integrate) each disk. This process is commonly called the method of disks.
The general formula for the method of disks is:
#V = int_a^b pi*(f(x))^2 dx#
where #f(x)# is the curve we're revolving about the x-axis, and #[a,b]# is the interval we're concerned with. Important to note is the #pi*(f(x))^2# - this just means "area of a circle with radius #f(x)#." Multiplying this by #dx# gives the volume of a cylinder (disk) of width #dx# and radius #dx#. And integration allows us to sum all these disks up, exactly what we want to accomplish.
So, in our case, we'll note that #f(x) = 2 - 2x#, and #[a,b] = [0,1]#, and substitute:
#V = int_0^1 pi*(2 - 2x)^2 dx#
Well, that was the difficult part; setting up the integral. From here, evaluating the integral should be fairly easy. I'll leave it to you as an exercise, but the answer should come out to
#V = (4pi)/3#


