Using the figure below, estimate the following?
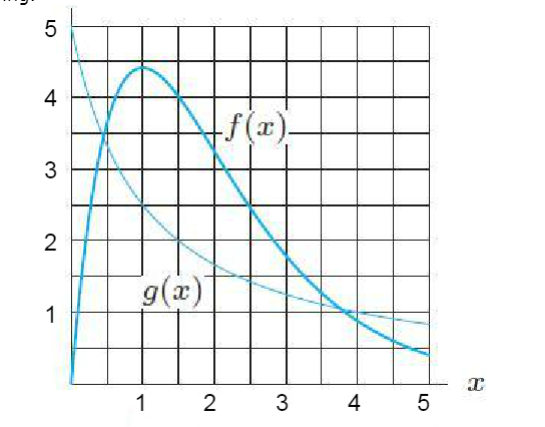 (a) f(g(2))=
(a) f(g(2))=
(b) g(f(2))=
(c) f(f(3))=
(d) g(g(3))=
I'm not exactly sure how to the values using this graph?
(a) f(g(2))=
(b) g(f(2))=
(c) f(f(3))=
(d) g(g(3))=
I'm not exactly sure how to the values using this graph?
1 Answer
a)
b)
c)
d)
Explanation:
For each of these, start from the innermost portion, find the value shown as the
f(g(2))
For this, start on the inside with
g(f(2))
First, approximate
f(f(3))
Start by using the graph to estimate
g(g(3))
Start by using the graph to estimate
