Question

Using the Schrodinger equation, what can we calculate?

Answer 1

In general, this equation is designed such that a unique Hamiltonian operator and wave function can be specified for a particular system. The most common thing we can obtain from the Schrodinger equation is the energy.

EXAMPLE

For example, take a single particle moving back and forth in a 1-dimensional box:

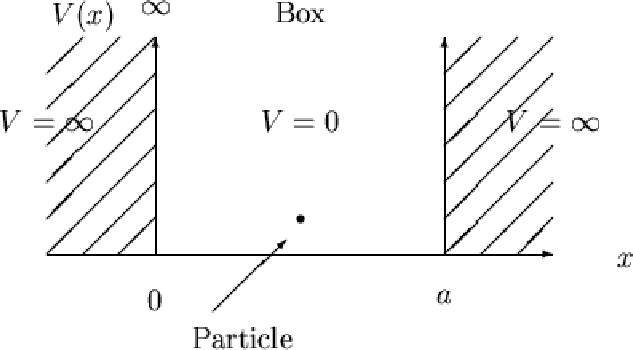
We start out with simply:

`hatHpsi = Epsi`

For this system, since the particle is said to move elastically horizontally, there is all kinetic and no potential energy.

The Hamiltonian is specified as:

`hatH = hatK + hatV`

`= -ℏ^2/(2m) grad^2 + V(x)`

where `grad^2 = (d^2)/(dx^2)`, the second derivative with respect to the `x` coordinate, the first overall term is the kinetic energy operator, and the potential is `V(x) = 0`.

OBTAINING THE SECOND-ORDER DIFFERENTIAL EQUATION

Plugging this into the starting equation, we solve for the second-order differential form of the Schrodinger equation for this system:

`-ℏ^2/(2m) d^2/(dx^2)psi(x) = Epsi(x)`

`(d^2psi(x))/(dx^2) = -(2mE)/(ℏ^2)psi(x)`

`bb((d^2psi(x))/(dx^2) + (2mE)/(ℏ^2)psi(x) = 0)`

This has now become a second-order differential equation for what is known as the particle in a box model, where the particle is in a well of infinite potential walls, with a closed interval `[0, a]`.

The above equation can be rewritten in an even more general form:

`(d^2psi(x))/(dx^2) + k^2psi(x) = 0`

SOLVING FOR k BY SETTING BOUNDARY CONDITIONS

The general solution to this situation for the wave function `psi` is:

`psi(x) = Acoskx + Bsinkx`,

where `k = sqrt((2mE)/ℏ^2)`.

The boundary conditions for this system must be set for it to be physically meaningful (the particle must vanish at the boundaries of the system).

In this case, `psi(0) = psi(a) = 0`. The first condition gives:

`psi(0) = Acos(0) + cancel(Bsin(0))^(0)`

In order for the whole thing to go to `0`, we know that `cos(0) = 1`, so we must force the condition by saying that `A = 0`.

The second (consecutive) condition gives:

`psi(a) = Bsin(ka)`

Here, the physically-meaningful and nontrivial solution is that `sin (ka) = 0`, and this is only if `ka = npi`.

USING k TO FIND THE ENERGY

Now if we plug back into the definition of `k`, where we now know that `k = (npi)/a` for this system:

`k = (npi)/a = sqrt((2mE)/(ℏ^2))`

`(n^2pi^2)/a^2 = (2mE)/(ℏ^2)`

`=> color(blue)(E_n = (n^2pi^2ℏ^2)/(2ma^2) = (n^2h^2)/(8ma^2))`

So this is the energy for a particle elastically traveling back and forth in a confined, 1D box.

(Surprisingly, this can be applied to real systems, like butadiene, for example, or other conjugated `pi` systems.)

---

For completion's sake, as a sidenote, we would also obtain `psi` for this system as:

`psi(x) = Bsin((npix)/a)`

and to get what `B` is, we normalize the wave function to get:

`1 = int_(0)^(a) psi^"*"(x)psi(x)dx`

`= int_(0)^(a)Bsin((npix)/a)Bsin((npix)/a)dx`

`= B^2 int_0^a sin^2((npix)/a)dx`

and eventually get that `B = sqrt(2/a)`, since `psi^2` must give a `100%` probability of finding this particle somewhere in this box.