Water is leaking out of an inverted conical tank at the rate of 10,000cm^3/min cm/min at the same time that water is being pumped into the tank at a constant rate. The tank has a height of 6m and the diameter at the top is 4m. If the water level is rising at a rate of 20 cm/min when the height of the water is 2m, how can I find the rate at which water is being pumped into the tank.?
1 Answer
(see below for solution method)
Explanation:
Start by ignoring the leakage and determine the rate of inflow required to achieve the specified rate of height (depth) of water increase.
Later we'll use the fact that
Actual inflow rate
= Inflow Rate for Increased Depth + Leakage Rate
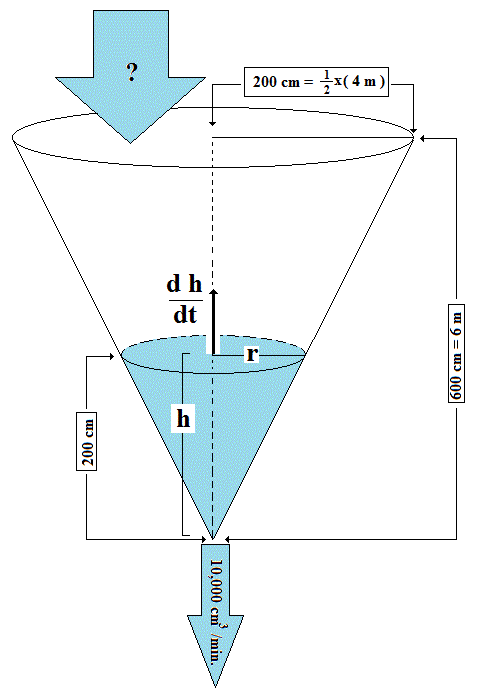
For the given cone the ratio of r adius to h eight is
so
The formula for the volume of a cone:
We are interested in the change in Volume with respect to time and note that
Using the value we've already calculated for
we get:
or roughly
This is the Inflow Rate Required to Cause Height Increase and
ignores the Rate of Leakage
The Actual Inflow Rate needs to be the sum of these two:

