We have #f:RR->RR;f(a)=int_0^1abs(x-a)dx#.What is minimum value of the function #f#?

Question

816 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-13T21:16:47

Please see the other correct answer by Cesareo.

Answer 2 · 2017-05-13T21:25:43

#f(1/2)=1/4#

With a change of variable #y = x-a#

#int_0^1 abs(x-a)dx equiv int_(-a)^(1-a) abs y dy = 1/2((1-a)^2"sign"(1-a)-a^2"sign"(-a)) = 1/2((1-a)^2"sign"(1-a)+a^2 "sign"(a))#

The minimum is located at #a=1/2# and #f(1/2)=1/4#

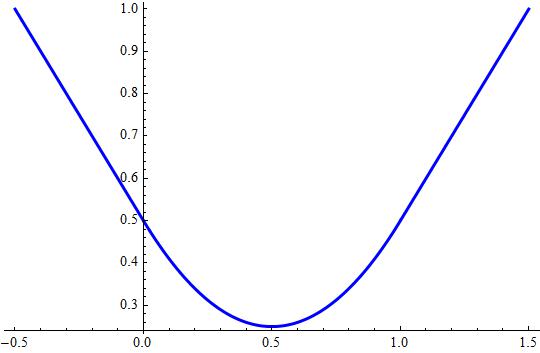
Attached a plot of #f(a)#

enter image source here