#d/(dx)(x( log_e x)^n)=n( log_e x)^(n-1)+( log_e x)^n#
but
#[x( log_e x)^n ]_1^e = e#
so
#n I_(n-1)+I_n = e# with #I_1 = int_1^e log_e xdx = 1#
The difference equation is a linear non-homogeneous one so it's solution can be written as
#I_n = I_n^h + I_n^p#
with
#n I_(n-1)^h+I_n^h = 0# and
#n I_(n-1)^p+I_n^p = e# ----- (*)
The homogeneous solution is
#I_n^h = (-1)^n n! C#
Making now #C = c_n# and substituting #I_n^p = c_n(-1)^n n! # into (*)
we obtain the recurrence law to #c_n# This is quite easy and is left to the reader.
The final solution is
#I_n =I_n^h+I_n^p =(-1)^n n! (e(sum_(k=0)^n (-1)^k/(k!))-1)#
NOTE:
#lim_(n->oo)sum_(k=0)^n (-1)^k/(k!) = e^-1#
so
#lim_(n->oo)I_n = 0#
NOTE:
Using Stirling's asymptotic formula
#n! approx sqrt(2 pi n)(n/e)^n# and calling #e_n = sum_(k=0)^n 1/(k!)# we have
#I_n approx (-1)^n sqrt(2 pi n)(n/e)^n((e-e_n)/e_n)=#
#= (-1)^n sqrt(2 pi n)(n/e)^n (sum_(k=n)^oo 1/(k!))/e_n =#
#= (-1)^n sqrt(2 pi n)/e_n (sum_(k=n)^oon^n/(k!))e^(-n)#
so
#lim_(n->oo)I_n = 0#
Attached plot showing the first #16# terms for #I_n#
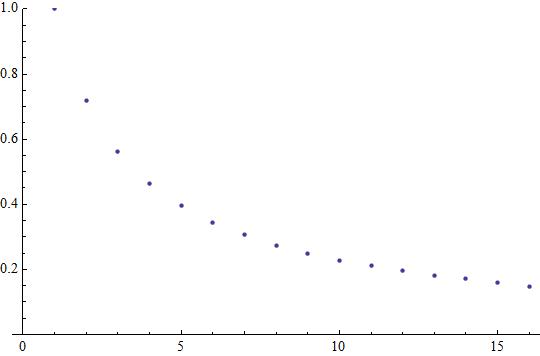
As we can observe #0 lt I_n le 1#


