What angle did the hawk make with the horizontal during its descent?

Question

What angle did the hawk make with the horizontal during its descent?

1 Answer

Impact of this question

1014 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-28T15:37:12

Please see below

Explanation:

Suppose,the mouse was released at point $A$ $A$ ,and then it travelled along the curved path $A C$ $AC$ , the hawk flew after the release upto $B$ $B$ for $2 s$ $2s$ ,and then followed along straight line $A C$ $AC$ ,to catch the mouse $3 m$ $3 m$ above the ground.

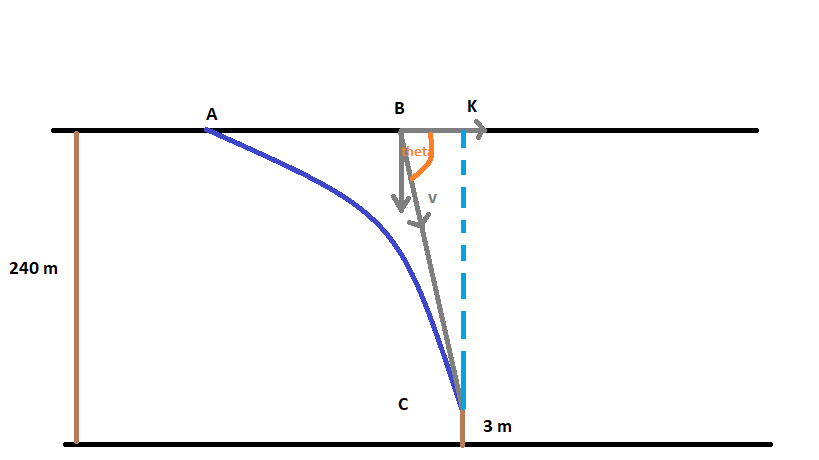
enter image source here

Now,when the mouse was released it had an initial horizontal velocity as same as that of the hawk,and due to the pull of the gravity it followed this parabolic path.

So,vertical length from $A$ $A$ to $C$ $C$ is $240 - 3 = 237 m$ $240-3 = 237 m$

So,for falling by this distance if the mouse took time $t$ $t$ ,then we can write,considering vertical motion only,

$237 = \frac{1}{2} g t^{2}$ $237 = 1/2 g t^2$ (using, $s = \frac{1}{2} g t^{2}$ $s= 1/2 g t^2$ )

So, $t = 6.94 s$ $t=6.94 s$

this is the time for which the mouse enjoyed free fall,

Now,in this time its horizontal displacement ( $A K$ $AK$ ) will be $19 \cdot 6.94 = 131.86 m$ $19*6.94=131.86 m$

Now,the question says,after releasing the mouse,the hawk went on flying with its initial velocity for $2 s$ $2s$ ,then followed this staright line pathway to catch the mouse at $C$ $C$ ,so it must cover pathway $A C$ $AC$ in $(6.94 - 2) = 4.94 s$ $(6.94-2)=4.94 s$

So,if it dived with velocity $v$ $v$ at an angle $θ$ $theta$ w.r.t horizontal,then it downward component of velocity is $v sin θ$ $v sin theta$ and horizontal component is $v cos θ$ $v cos theta$

So,again considering vertical motion only for the hawk,we can say,

$237 = v sin θ \cdot 4.94 + \frac{1}{2} {g (4.94)}^{2}$ $237 = v sin theta * 4.94 + 1/2 g (4.94)^2$ (using, $s = u t + \frac{1}{2} g t^{2}$ $s= ut + 1/2g t^2$ )

so, $v sin θ = 23.75$ $v sin theta=23.75$

Again in this time the hawk will also have a horizontal displacement of $131.86 m$ $131.86 m$ (as same as that of the mouse)

But it went from $A$ $A$ to $B$ $B$ with its initial velocity,then with velocity $v cos θ$ $v cos theta$

So, $A K = A B + B K = (19 \cdot 2) + (v cos θ \cdot 4.94) = 131.86$ $AK = AB + BK = (19*2) +(v cos theta*4.94)=131.86$

So, $v cos θ = 19$ $v cos theta =19$

So, $v^{2} {sin}^{2} θ + v^{2} {cos}^{2} θ = {(23.75)}^{2} + {(19)}^{2}$ $v^2 sin^2 theta + v^2 cos ^2 theta = (23.75)^2 + (19)^2$

So, $v = 30.42 m s^{- 1}$ $v=30.42 ms^-1$

So, we can say, $30.42 \cdot cos θ = 19$ $30.42*cos theta = 19$

or, $θ = {cos}^{- 1} (\frac{19}{30.42}) = {51.35}^{\circ}$ $theta = cos ^-1(19/30.42)=51.35 ^@$

Science

Math

Humanities

... and beyond

What angle did the hawk make with the horizontal during its descent?

1 Answer

Explanation:

Related questions

Impact of this question