What are all the possible rational zeros for f(x)=x^5-6x^4+12x^2-8x+36 and how do you find all zeros?
1 Answer
Find there are no rational zeros. Use a numerical method to find approximations.
Explanation:
By the rational roots theorem, any rational zeros of
That means that the only possible rational zeros are:
+-1, +-2, +-3, +-4, +-6, +-9, +-12, +-18, +-36
None of these works, so
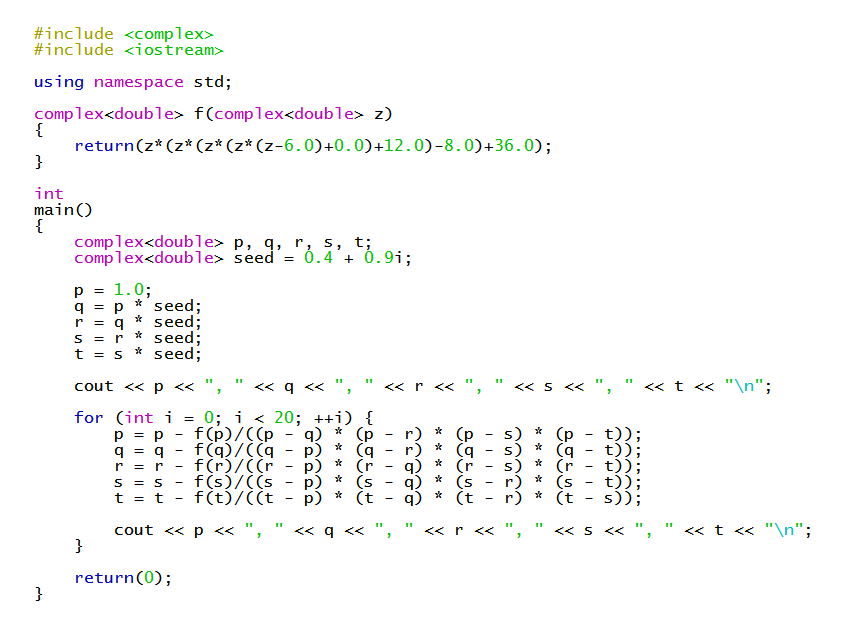
About the best we can do is use the Durand-Kerner or similar numerical method to find approximations:
x_1 ~~ 5.63048
x_2 ~~ 2.05347
x_3 ~~ -1.84949
x_(4,5) ~~ 0.0827684+-1.29486i
See https://socratic.org/s/axpvv6Hk for some more description of the method.
For the current example, the above approximations were found using this C++ program...