Question

What are coulombic and exchange energy and how are they determined?

Answer 1

A simplified way is to call them `Pi_c` and `Pi_e`, the coulombic and exchange components of the pairing energy `Pi`:

`Pi = Pi_c + Pi_e`


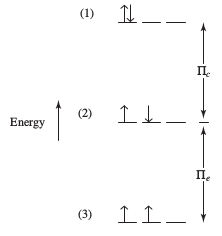
[This is gone into more detail here.]

For example, consider the ground state valence configuration of chromium:

`ul(uarr color(white)(darr))`
`4s`

`underbrace(ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr)))`
`" "" "" "" "" "" "color(white)(/)3d`

This has zero coulombic repulsion energy `Pi_c`, because no electrons are paired. However, if we focus on the `3d` electrons, there are `10` possible nonredundant exchanges.

Label each electron to get:

`uarr_1 uarr_2 uarr_3 uarr _4 uarr_5`

Now, the possible exchanges (that result in the same energy) involve all of the `3d` electrons:

`1harr{2, 3, 4, 5}` `->` `4` exchanges
`2harr{3, 4, 5}` `->` `3` exchanges
`3harr{4, 5}` `->` `2` exchanges
`4harr{5}` `->` `1` exchange

(Try not to double-count; so don't count `1harr2` and then `2harr1`; those are the same thing.)

This is true because all of the electrons are all indistinguishable. This results in an exchange energy stabilization of `10xxPi_e` (meaning `Pi_e < 0`), one for each exchange.

So the pairing energy in total is:

`Pi = 10Pi_e`

Now, suppose instead, the chromium atom was in this state:

`ul(uarr darr)`
`4s`

`underbrace(ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(color(white)(uarr darr)))`
`" "" "" "" "" "" "color(white)(/)3d`

Now there is one pair of electrons that ARE repelling each other, so the coulombic repulsion energy is `1xxPi_c`. However, the exchange energy stabilization now is only `6 xx Pi_e`...

So the pairing energy in total is higher than before:

`Pi = Pi_c + 6Pi_e`

This is less stable by `Pi_c - 4Pi_e`, and qualitatively shows that chromium should "prefer" the `3d^5 4s^1` configuration over the `3d^4 4s^2` configuration.

This approach also explains why tungsten prefers a `5d^4 6s^2` configuration.