What are invertible functions? plz explain.
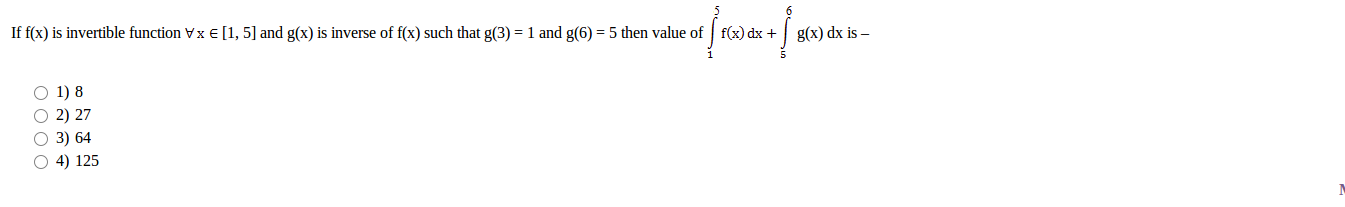
1 Answer
See explanation...
Explanation:
There are at least two things implied by the assertion:
"
#f(x)# is invertible function#AA x in [1, 5]# "
-
#f(x)# is a function with domain including all of the real interval#[1, 5]# -
For any
#x_1, x_2 in [1, 5]# we have#f(x_1) = f(x_2) => x_1 = x_2# . In other words,#f(x)# is one to one.
Considered as a function on the domain
#g(f(x)) = x" "# for all#x in [1, 5]#
#f(g(x)) = x" "# for all#x in f("["1, 5"]")#
We are not told anything about the behaviour of
For the purposes of the rest of the question we do not care.
Given:
#g(3) = 1# and#g(6) = 5#
we can deduce:
#f(1) = 3# and#f(5) = 6#
If the question is correct - which I am not sure - then we can find which multiple choice option is correct by using a linear function for
Let:
#f(x) = 3/4(x-1)+3 = 3/4x+9/4#
#g(x) = 4/3(x-3)+1 = 4/3x-3#
Integrate each one the given intervals and add to find the answer.
I think the question is flawed in at least a couple of ways:
-
The integration limits for
#g(x)# should be#color(red)(3)# and#6# , not#5# and#6# . -
Some extra conditions on the functions are required to make them integrable. For example, we could specify that
#f(x)# is continuous.
With the question corrected, the answer I would expect would be the sum of the areas of three rectangles:
-
Vertices
#(1, 0), (5, 0), (5, 3), (1, 3)# with area#4*3 = 12# -
Vertices
#(1, 3), (5, 3), (5, 6), (1, 6)# with area#4*3 = 12# -
Vertices
#(0, 3), (1, 3), (1, 6), (0, 6)# with area#1*3 = 3#
So, total

