Question

What are scientific models?

Answer 1

Scientific models are objects or concepts constructed to explain phenomena that may not be technically observable.

Even in higher levels of chemistry, models are very useful, and are often constructed to estimate chemical properties. An example below illustrates the use of models to estimate a known quantity.

---

Suppose we want to model benzene, `"C"_6"H"_6`, to estimate the wavelength for its strongest electronic transition:

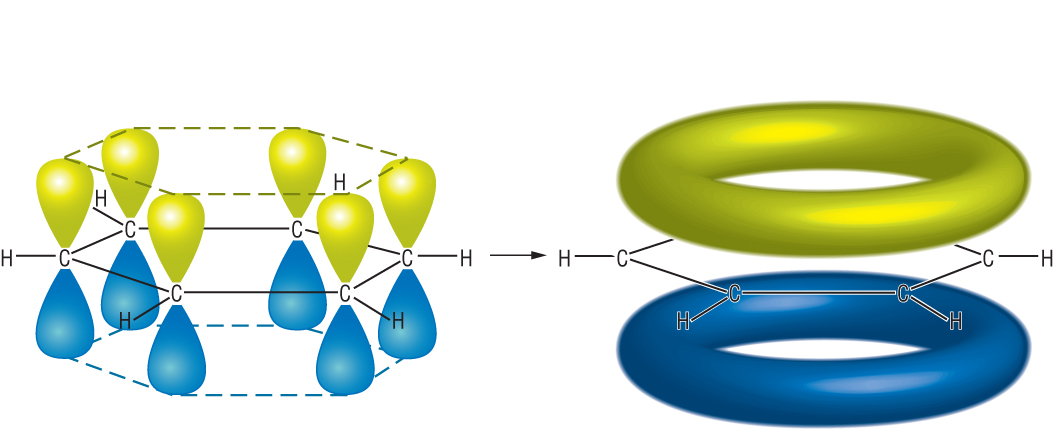
The true value is `"180 nm"` for the `pi_2->pi_4^"*"` or `pi_3->pi_5^"*"` transition. Let's see how close we get.

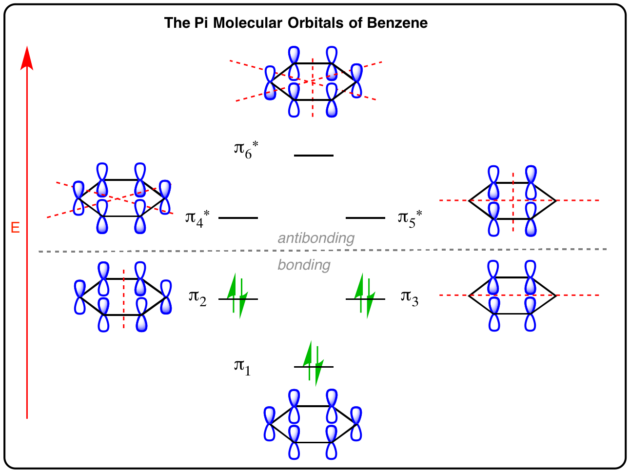
MODEL 1: PARTICLE ON A RING

The Particle on a Ring model is useful for describing the `pi` system of benzene, by modeling the `pi` electrons on the circumference of the `pi` electron cloud:

The energy levels are:

`E_k = (ℏ^2k^2)/(2I)`, `" "k = 0, pm1, pm2, . . .`

where:

• `I = m_eR^2` is the moment of inertia for the particle as a point mass a constant radial distance `R` away from `O`.
• `k = sqrt((2IE)/ℏ^2)` is the quantum number for this system.
• `ℏ = (6.626 xx 10^(-34) "J"cdot"s")/(2pi)` is the reduced Planck's constant.
• `m_e = 9.109 xx 10^(-31) "kg"` is the mass if an electron is the particle.
• `c = 2.998 xx 10^8"m/s"`, the speed of light, will be needed.

The strongest electronic transition corresponds to `E_1` to `E_2`:

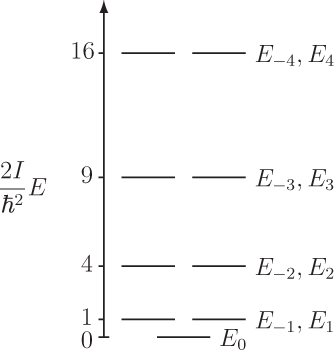
If we use this knowledge, we can estimate the wavelength observed for the strongest electronic transition. It is known experimentally that `R = 1.40 xx 10^(-10) "m"`.

The energy gap is:

`DeltaE_(1->2) = ℏ^2/(2I)(2^2 - 1^2)`

From the relation that `DeltaE = hnu = hc//lambda`:

`color(blue)(lambda) = (hc)/(DeltaE) ~~ (hc)/(DeltaE_k) = (hc cdot 2m_eR^2)/(ℏ^2(2^2 - 1^2))`

`= (4pi^2 cdot hc cdot 2m_eR^2)/(3h^2)`

`= (8pi^2 cm_eR^2)/(3h)`

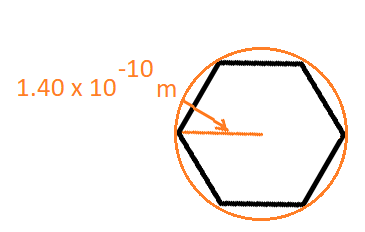
`= (8pi^2 cdot 2.998 xx 10^8 "m/s" cdot 9.109 xx 10^(-31) "kg" cdot (1.40 xx 10^(-10) "m")^2)/(3(6.626 xx 10^(-34) "J"cdot"s"))`

`= 2.13 xx 10^(-7) "m"`

`=` `color(blue)("213 nm")`

MODEL 2: PARTICLE IN A BOX

The Particle in a Box model can also be used for the same purpose. We can confine benzene into a `2.80 xx 10^(-10) "m"` by `2.80 xx 10^(-10) "m"` box.

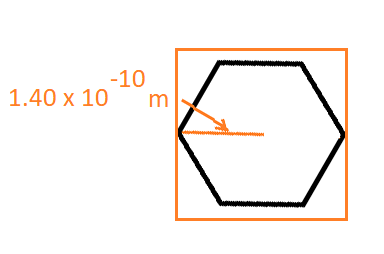
In two dimensions, the energy levels are:

`E_(n_xn_y) = (h^2)/(8m_e)[n_x^2/L_x^2 + n_y^2/L_y^2]`,

`n_x = 1, 2, 3, . . .`
`n_y = 1, 2, 3, . . .`

The first few are:

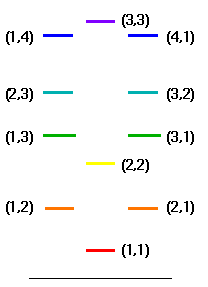
which matches the way the energy levels are in benzene exactly, if we call `E_22` the nonbonding level. From this,

`DeltaE_(12 -> 13) = (h^2)/(8m_e)[(cancel(1^2/L_x^2) + 3^2/L_y^2) - (cancel(1^2/L_x^2) + 2^2/L_y^2)]`

`= (h^2)/(8m_e)((3^2 - 2^2)/L_y^2)`

`= (6.626 xx 10^(-34)"J"cdot"s")^2/(8cdot9.109 xx 10^(-31) "kg")((3^2 - 2^2)/(2.80 xx 10^(-10) "m")^2)`

`= 3.84 xx 10^(-18) "J"`

And so, the wavelength involved is estimated to be:

`color(blue)(lambda) = (hc)/(DeltaE_(12->13)) = (6.626 xx 10^(-34) "J"cdot"s" cdot 2.998 xx 10^8 "m/s")/(3.84 xx 10^(-18) "J")`

`= 5.17 xx 10^(-8) "m"`

`=` `color(blue)"51.7 nm"`

So as it turns out, the particle on a ring is more effective of a model for benzene.