What are the critical points, if any, of #f(x,y) = 2x^3 - 6x^2 + y^3 + 3y^2 - 48x - 45y#?
1 Answer
# {: (f(-2,-5),= 231,=>(-2,-5,231)), (f(-2,3),= -25,=>(-2,3,25)), (f(4,-5),= 15,=>(4,-5,15)), (f(4,3), = -241,=>(4,3,-241)) :} #
Explanation:
The theory to identify the extrema of
- Solve simultaneously the critical equations
# (partial f) / (partial x) =(partial f) / (partial y) =0 \ \ \ # (ie#f_x=f_y=0# ) - Evaluate
#f_(x x), f_(yy)# and#f_(xy) (=f_(yx))# at each of these critical points. Hence evaluate#Delta=f_(x x)f_(yy)-f_(xy)^2# at each of these points - Determine the nature of the extrema;
# {: (Delta>0, "There is minimum if " f_(x x)>0),(, "and a maximum if " f_(x x)<0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :} #
So we have:
# f(x,y) = 2x^3 - 6x^2 + y^3 + 3y^2 - 48x - 45y #
Let us find the first partial derivatives:
# (partial f) / (partial x) = 6x^2-12x-48 #
# (partial f) / (partial y) = 3y^2+6y-45 #
So our critical simultaneous equations are:
# (partial f) / (partial x) = 0 => 6x^2-12x-48 = 0 #
# (partial f) / (partial y) = 0 => 3y^2+6y-45 = 0 #
# :. x^2 - 2x - 8 = 0 #
# :. (x-4)(x+2) = 0 #
# :. x = -2, 4 #
# :. y^2 + 2y - 15 = 0 #
# :. (y+5)(y-3) = 0 #
# :. y = -5, 3 #
Any permutation of these solutions will simultaneously make both partial derivatives vanish, so the critical values are:
#(x,y)=(-2,-5), (-2,3), (4,-5), (4,3) #
So we can now calculate the coordinates of the critical points:
# {: (f(-2,-5),= 231,=>(-2,-5,231)), (f(-2,3),= -25,=>(-2,3,25)), (f(4,-5),= 15,=>(4,-5,15)), (f(4,3), = -241,=>(4,3,-241)) :} #
We can visualise these critical points on a 3D-plot:
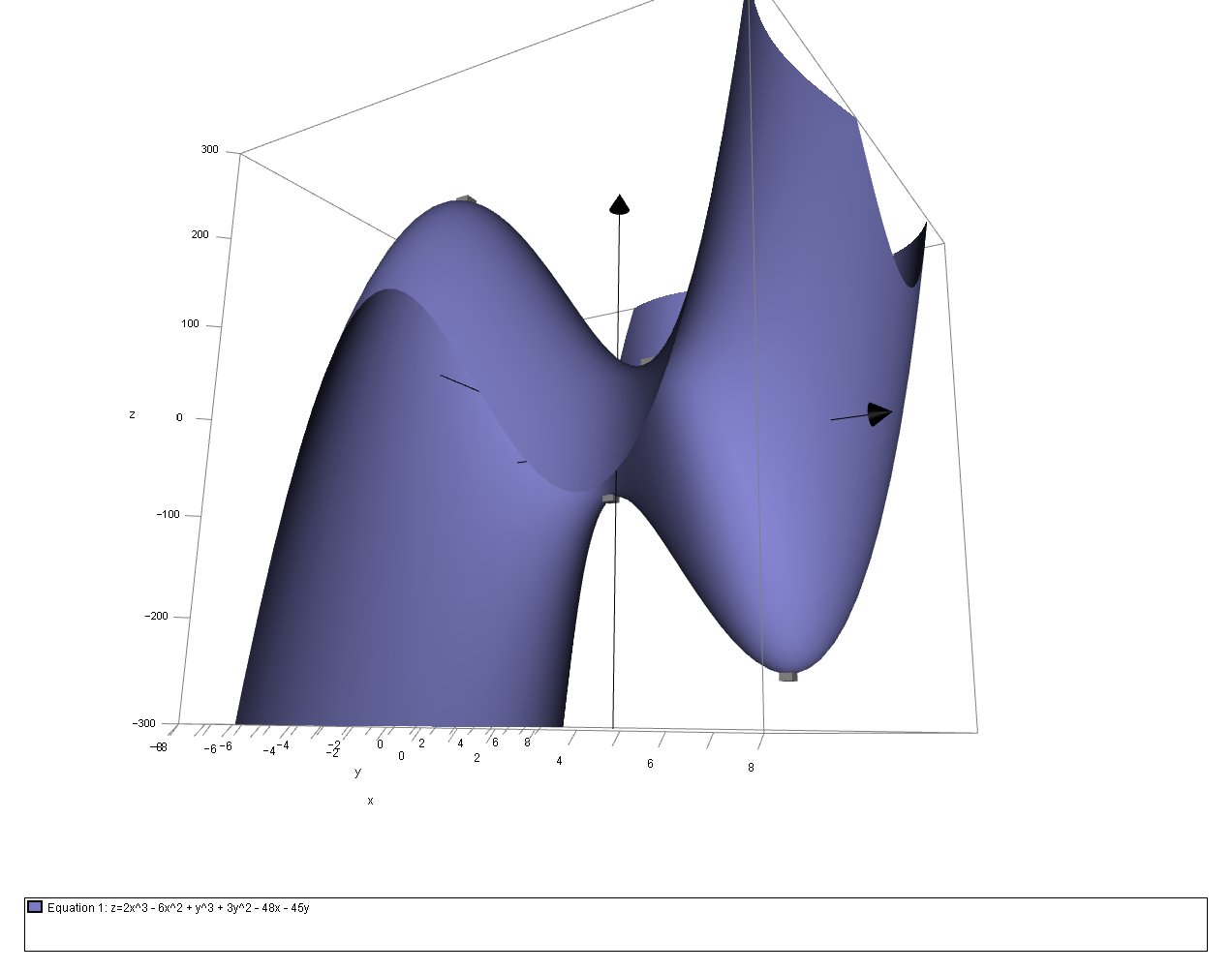
As we were not asked to determine the nature of the critical points I will omit that analysis.

