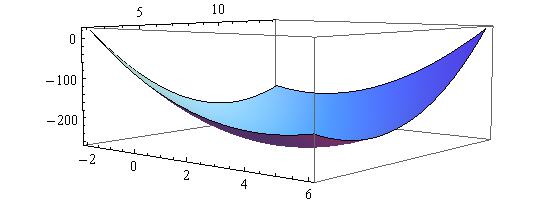
What are the critical points, if any, of #f(x,y) = 5x^2 + 4xy + 3y^2 - 52x - 56y + 13#?

Question

1856 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-07T11:37:50

#f(x,y)# has a local minimum point at #{x=2, y = 8}#

We will determine the stationary points instead. Those points observe the condition

#grad f(x,y)= vec 0#

In the present case we have

#grad f(x,y) = {(partial f)/(partial x),(partial f)/(partial y)} = {-52 + 10 x + 4 y, -56 + 4 x + 6 y} #

and for stationary points determination

# { (-52 + 10 x + 4 y = 0), (-56 + 4 x + 6 y=0) :} #

solving for #x, y# we have

#{x=2, y = 8}#

Point qualification is obtained by computing

#grad^2f(x,y) = ((f_{x x},f_{xy}),(f_{yx},f_{yy}))#

In this point we have

#grad^2f(2,8) = ((10,4),(4,6))#

This matrix is positive definite because it have two positive eigenvalues #{2 (4 + sqrt[5]), 2 (4 - sqrt[5])}# so the point is a local minimum point.

enter image source here