Question

What are the perihelion and aphelion speeds of Mercury? What are the perihelion and aphelion distances of Earth? How would these speeds be calculated?

Answer 1

I suppose you wanted the speeds for both Earth AND Mercury.

Explanation:

I would use the radial distances `r` both at perihelion `P` and aphelion `A` into Newton's Second Law `Sigmavec(F)=mvec(a)` using also centripetal acceleration:

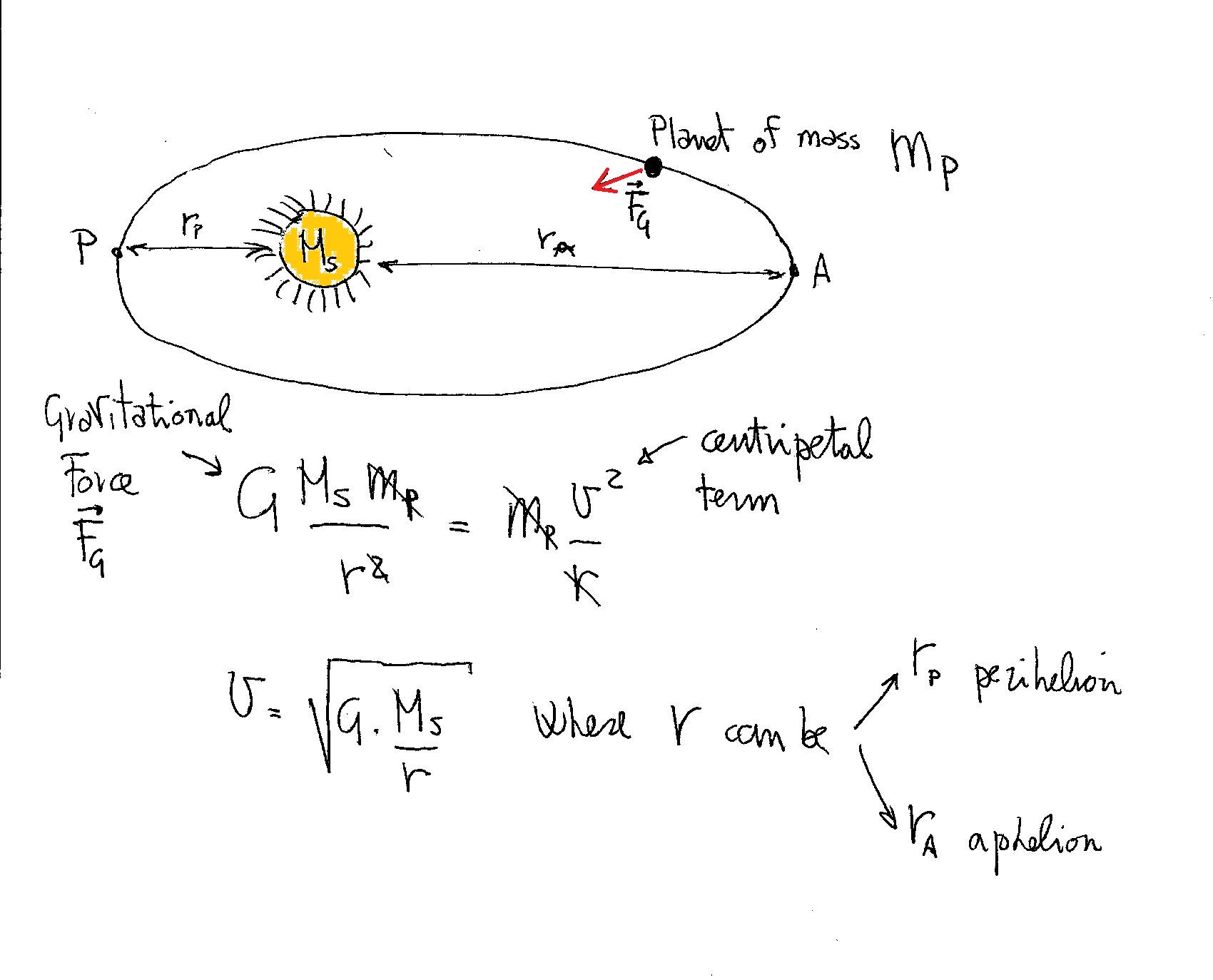
Use the values from the literature for the mass of the Sun, `M_S`, `G`, and the radial distances (you may find them in books, I think).

Answer 2

Mercury;s perihelion speed = 69.8 km's and aphelion speed is 46.0 km/s. Earth's perihelion = 147.1 million km and aphelion = 152.1 million km.

Explanation:

Let `v_a` = speed , when the distance of a planet from the Sun is the semi-major axis a of the planet's orbit., `v_(pe)` = perihelion speed and`v_(ap)` = speed at aphelion. Let e be the eccentricity of the orbit.

Then, approximating `v_a` = average speed v,

`v_(pe)=v_a(1+e)=v(1+e)`, nearly and `v_(ap)=v_a(1-e)=v(1-e)`, nearly.

I can assure you that these approximations give 3-sd values without error, if there are no bugs in the data used..

For Mercury v = 47.4 km/s, a = 57.9 million (M) km and e = 0.2055. .

So, `v_(pe)=47.4(1+0.2055)=69.8 km/s` and
`v_(ap)=47.4(1-0.2055)=46.0` km/s#, nearly.

This way, the perihelion and aphelion speeds of the Earth can be approximated using relevant data from sources like
NASA Planetary Fact Sheet.