Question

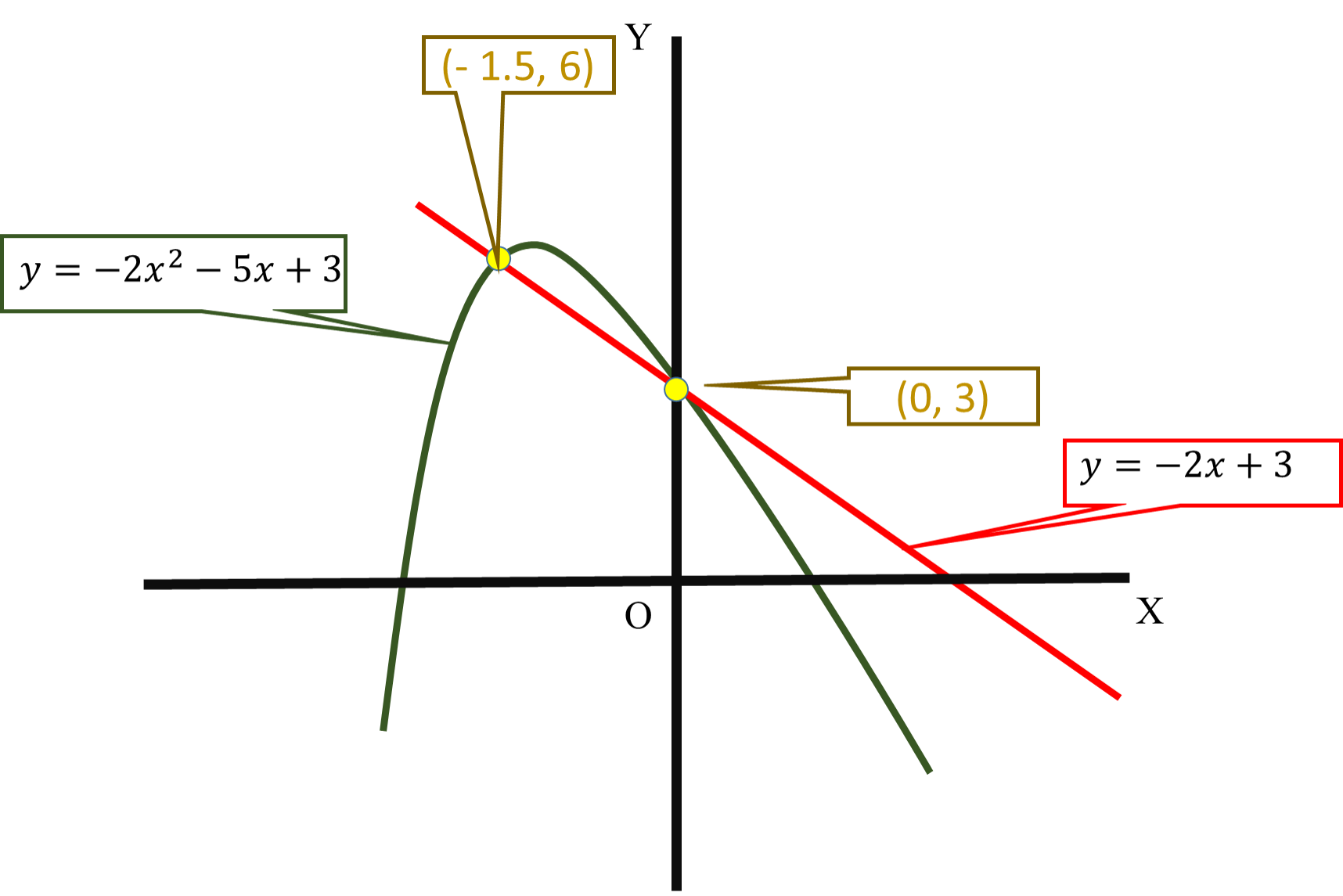
What are the points of intersection of `y=-2x^2-5x+3` and `y=-2x+3`?

Answer 1

`(0,3), and, (-3/2,6)`.

Explanation:

To find the pts. of intersection of these two curves, we have to solve

their eqns.

`y=-2x^2-5x+3, and, y=-2x+3`

`:. -2x+3=-2x^2-5x+3, or, 2x^2+3x=0`

`:. x(2x+3)=0`

`:. x=0, x=-3/2`

`:. y=-2x+3=3, y=6`

These roots satisfy the given eqns.

Hence, the desired pts. of int. are `(0,3), and, (-3/2,6)`.

Answer 2

At points `(0, 3); (-1.5, 6)` the two curves intersets

Explanation:

Given -

`y=-2x^2-5x+3`
`y=-2x+3`

To find the intersection point of these two curves, set -

`-2x^2-5x+3=-2x+3`

Solve it for `x`

You will get at what values of `x` these two intersect

`-2x^2-5x+3+2x-3=0`
`-2x^2-3x=0`
`x(-2x-3)=0`
`x=0`
`x=3/(-2)=-1.5`

When `x`takes the values 0 and - 1.5 the two intersects

To find the point of intersection, we must know the Y-cordinate

Substitute `x` in any one of the equations.

`y=-2(0)+3`
`y=3`

At `(0, 3)` the two curves intersets

`y=-2(1.5)+3=3+3=6`

At `(-1.5, 6)` the two curves intersects