What are the possible rational roots of 6x^4+35x^3-x^2-7x-1=0 and then determine the rational roots?
1 Answer
Jan 9, 2017
The possible rational roots are
The rational roots are
Explanation:
The possible rational roots are obtained by dividing each of the factors of the known term (-1) by each of the factors of the maximum degree term's coefficient (6).
Then they are:
To determine the rational roots, let's use the remainder rule:
Then
You also can use a spreadsheet to find zeros faster.
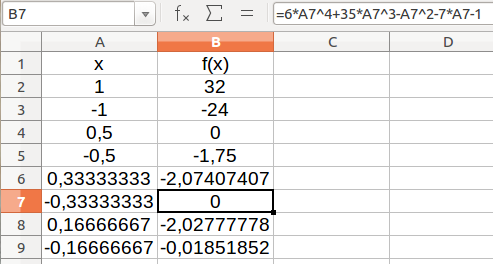
Then you would find only another rational root

