.
To find the extrema of the function, we need to find its derivative, set it equal to zero, and find its roots:
#f(x,y)=8x^4+y^2-24xy#
#f'(x,y)=32x^3dx+2ydy-24xdy-24ydx=0#
#dy(2y-24x)-dx(32x^3-24y)=0#
#dy(2y-24x)=dx(32x^3-24y)#
#dy/dx=(32x^3-24y)/(2y-24x)=(16x^3-12y)/(y-12x)=0#
#16x^3-12y=0#
#16x^3=12y#
#4x^3=3y#
#y=4/3x^3#
At #y=4/3x^3#, the function has maximum(s) and minimum(s). To find the coordinates of these points, we set this function equal to #f(x,y)#, i.e. we plug #4/3x^3#: in for #y#
#8x^4+(4/3x^3)^2-24x(4/3x^3)=0#
#8x^4+16/9x^6-32x^4=0#
#16/9x^6-24x^4=0#
#x^4(16/9x^2-24)=0#
#x=0#
#16/9x^2=24#
#x^2=24(9/16)=27/2#
#x=+-(3sqrt6)/2#
#y=4/3(+-(3sqrt6)/2)^3=+-27sqrt6#
#((3sqrt6)/2, 27sqrt6)# is the relative maximum
#(-(3sqrt6)/2, -27sqrt6)# is the relative minimum
Notice the denominator of #dy/dx#. If we set it equal to zero and solve for its roots we will find the points where the derivative is undefined.
To find the coordinates of these points, we set this function equal to #f(x,y)#:
#y-12x=0#
#y=12x#
#8x^4+(12x)^2-24x(12x)=0#
#8x^4+144x^2-288x^2=0#
#8x^4-144x^2=0#
#8x^2(x^2-18)=0#
#x=0#
#x=+-3sqrt2#
At #x=0, 3sqrt2, and -3sqrt2# the derivative and the function are undefined. This means the function has a hole at each of these points.
At the holes, the function is discontinuous and presumably goes to infinity, which is the reason why the extrema are considered relative not absolute.
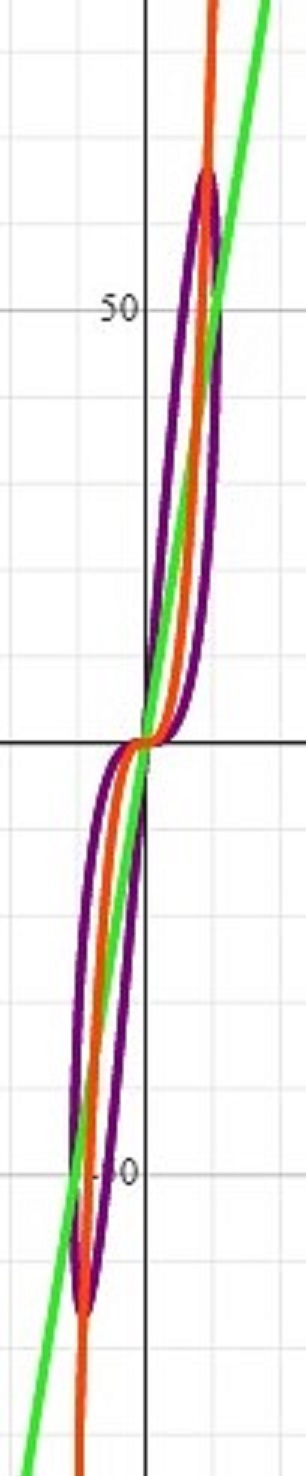
Here is the graph of the function:
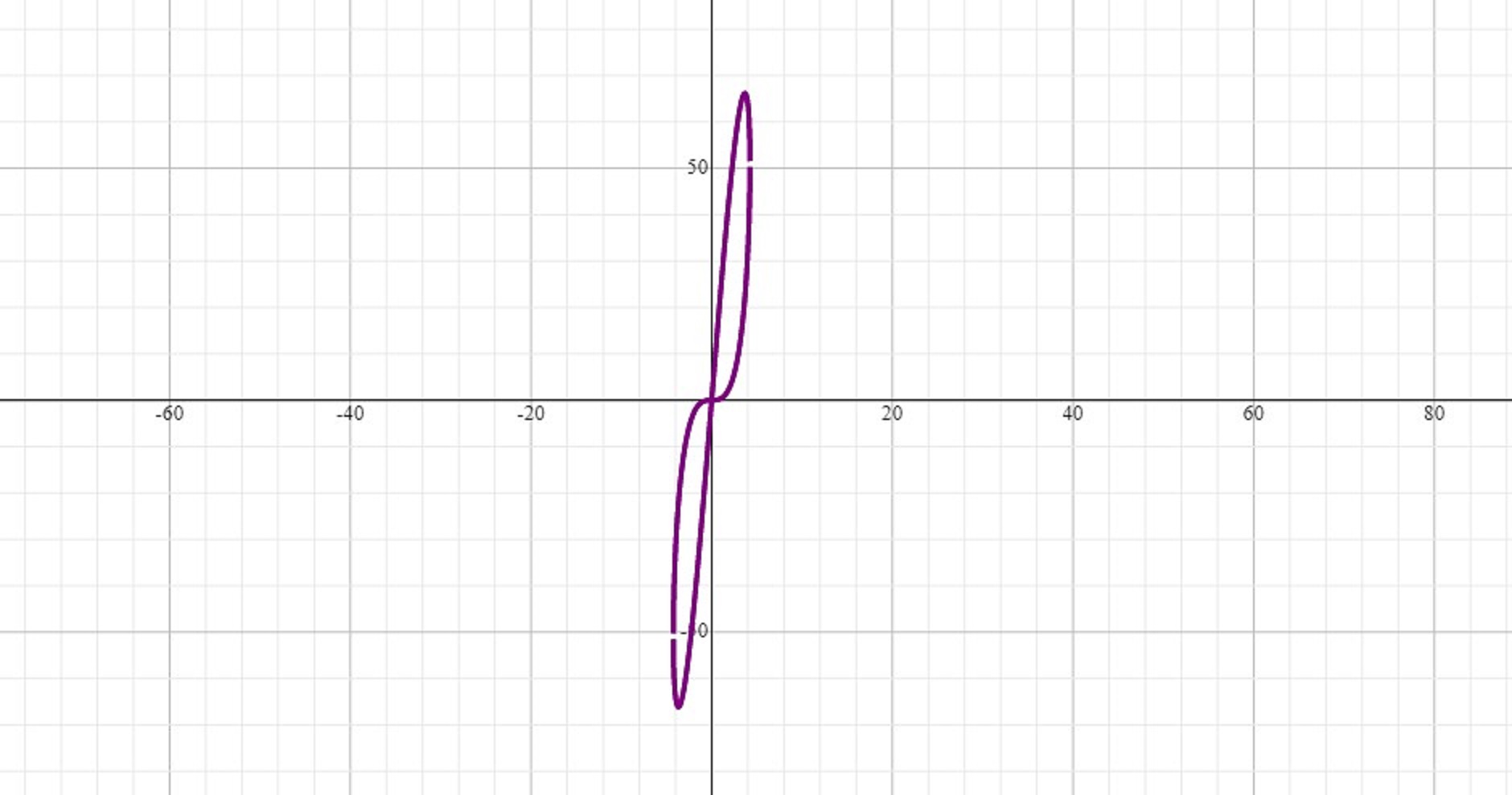
Here is a blow up of it that shows the holes better:

This is how we found the extrema and the holes of the function when we set the various functions equal to each other and found the intersection points:
#f(x.y)# is shown in purple.
#y=4/3x^3# is shown in red.
#y=12x# is shown in green.
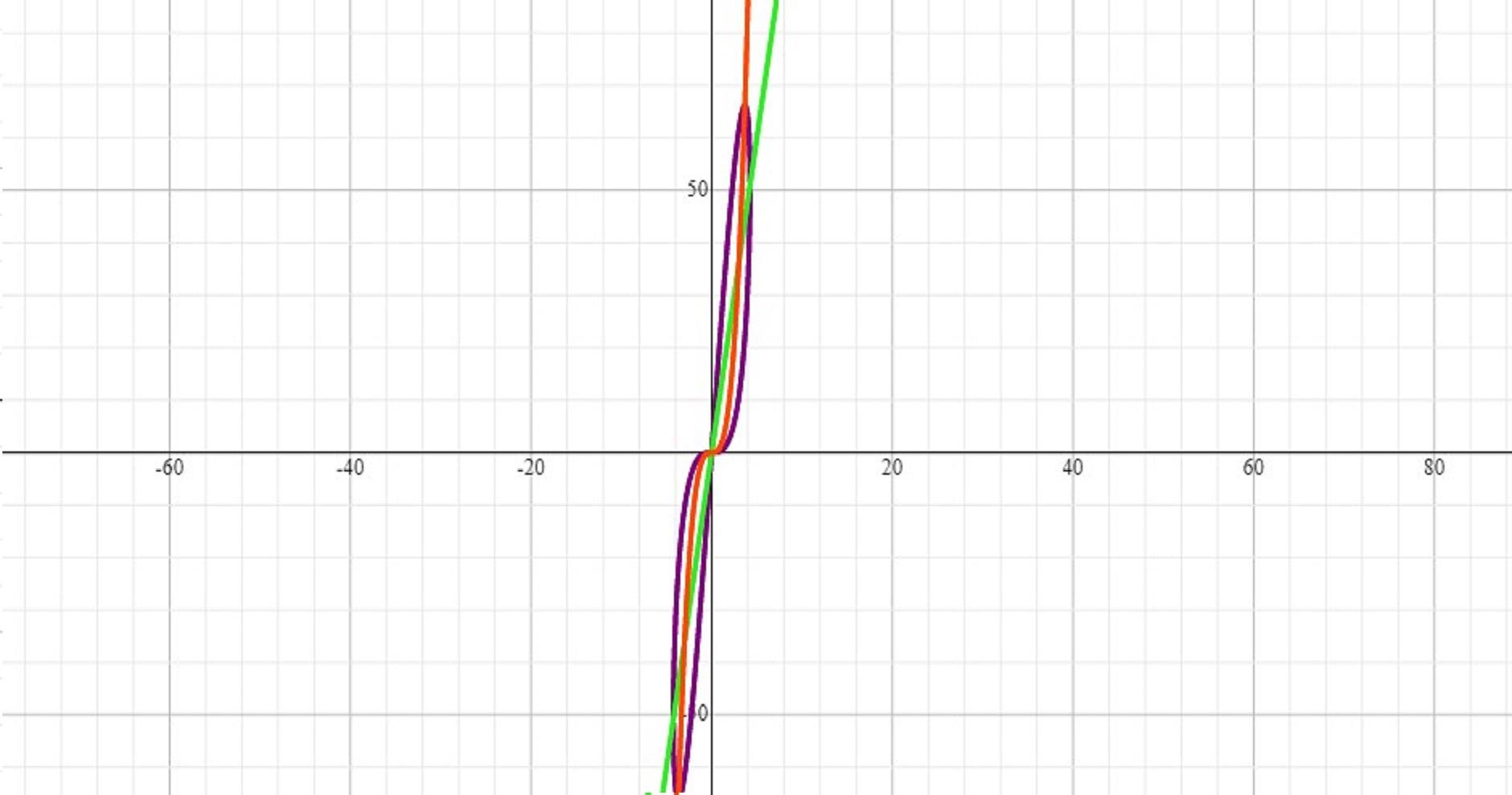
Here is a blow up of it: