Question

What are the x and y intercepts of the equation?

Answer 1

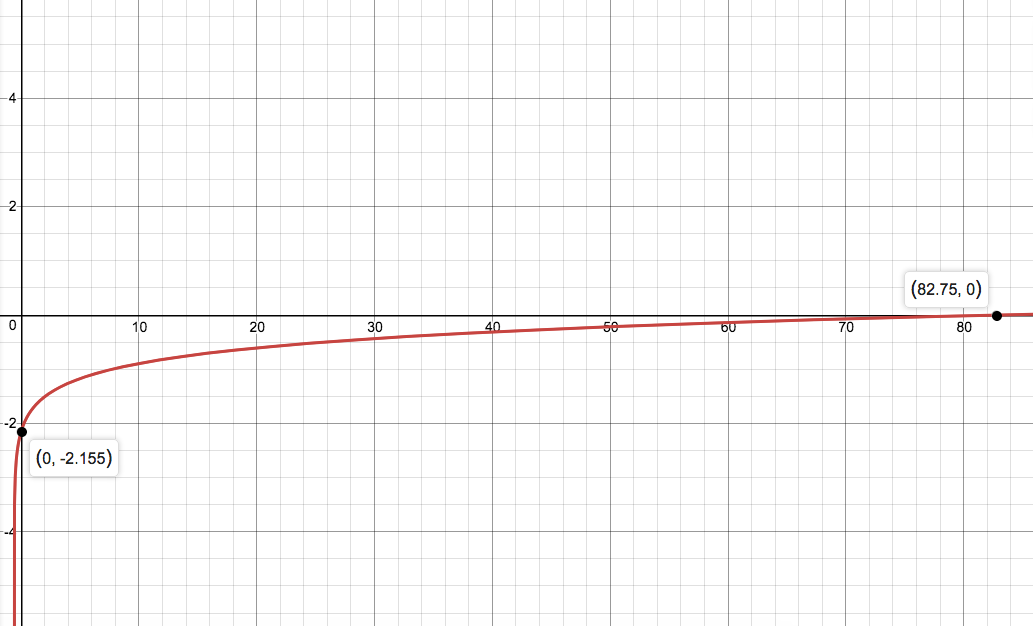
Intercepts:

`x: (82.75,0)`

`y:(0,log(7)-3 )`

Explanation:

To answer this problem we must be able to find the intercepts, by considering:

The `y` intercept is when the functions crosses the `y` axis
`=> x = 0`

At `x = 0 => y = log(7) - 3`

The `x` intercept is when the functions crosses the `x` axis
`=> y = 0`

`=> log(12x+7) - 3 = 0`

Rearanging:

`=> log(12x+7) = 3`

Using our log laws:

`10^log(x) -= x`

`=> 10^log(12x+7) = 10^3`

`=> 12x + 7 = 10^3`

`=> 12x = 10^3 - 7`

`=> x = 1/12 ( 10^3 - 7 ) = 82.75`

Answer 2

See below.

Explanation:

I am assuming these are base 10 logarithms.

`y` axis intercepts occur when `x=0`

`y=log(12(0)+7)-3=> y =log(7)-3~~-2.155` ( 3 .d.p.)

`x` axis intercepts occur when `y =0`

`log(12x+7)-3=0`

`log(12x+7)=3`

Raising to the power of 10: ( antilogarithm )

`10^(log(12x+7))=10^3`

`12x+7=1000`

`x=993/12=82.75color(white)(888)`

`x` intercept `( 82.75,0)`

`y` intercept `( 0 ,-2.155)`