What can be the least energy of a system as per Heisenberg's uncertainty principle?
1 Answer
Depends on the system... but if we are telling the whole truth, then it would be a zero minimum energy that isn't possible.
Even though the rigid rotator has zero energy in the ground state, it is not violating the Uncertainty Principle because it also translates in space and its total energy is unstated.
- An electron in a one-dimensional box of length
#a# CANNOT have zero energy:
#E_n = (n^2pi^2ℏ^2)/(2ma^2)# ,#n = 1, 2, 3, . . . #
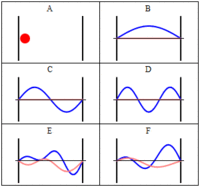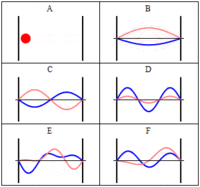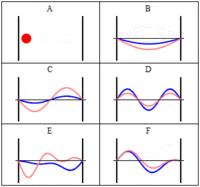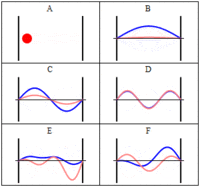
If it did, that would require that it have zero velocity, which means it has well-known momentum, which means it has POORLY known position, as per Heisenberg's Uncertainty Principle. But that means it ISN'T trapped in the box of length
#a# that it IS (by construction) trapped in.So we have concluded that zero energy
#-># the particle doesn't exist in the box, i.e. the system does not exist.
- A harmonic oscillator CANNOT have zero energy:
#E_upsilon = ℏomega(upsilon + 1/2)# ,#upsilon = 0, 1, 2, . . . # It has a zero-point energy of
#E_0 = 1/2ℏomega# , which is positive.
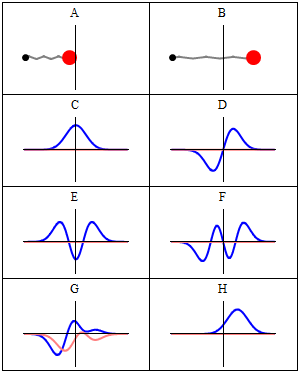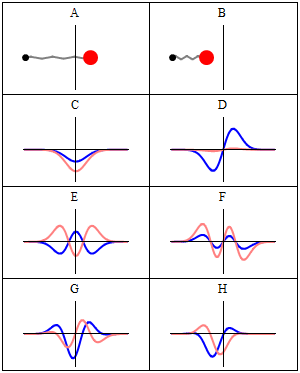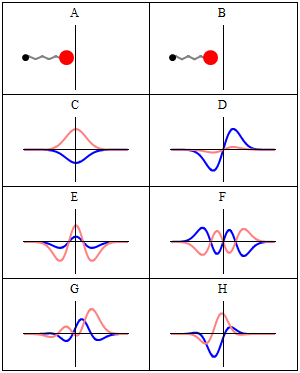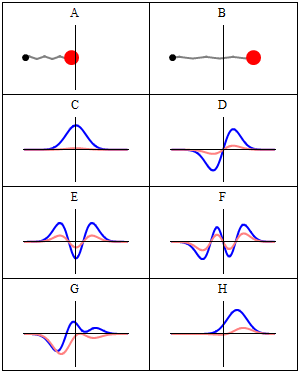
Zero energy would mean it has zero frequency, and thus that the oscillator is not moving. But again, that would suggest that its momentum is well-known, which would suggest its position is NOT, as per Heisenberg's Uncertainty Principle... even when it is not moving and its position IS well-known.
Thus, we have a contradiction and the system cannot exist if it is to have
#E = 0# .
- A rigid rotator CAN have zero energy (but this is a straight-up lie), and does NOT violate the Heisenberg Uncertainty Principle as we can only calculate rotational energy for this system (hence, nothing is stated about the translational kinetic energy, which can be nonzero, so that momentum is nonzero):
#E_J = hcBJ(J+1)# ,#J = 0, 1, 2, 3, . . . #
This is confidently stated here in this book. I believe it, as again, the translational energy from the Schrodinger equation of this system has to be stated by the person who constructed the system.
At a rotational quantum level
#J = 0# , the ground-state rotational energy is#E_0 = hcBJ(J+1) = 0# .However, the wave function at
#J = 0# is a constant (zero angular momentum), and being only a function of rotation angles, does not give information about the linear momentum (i.e. the translational kinetic energy is unstated).This is because in solving the rigid rotator system, we separate out the total wave function into an arbitrary translational part
#psi(r)# (which just gives a phase factor to the total wave function#psi(r,theta,phi# )) and a solvable rotational part#psi(theta,phi)# .Hence, we are not claiming certainty about linear momentum or position, which is not breaking the Uncertainty Principle.

