Question

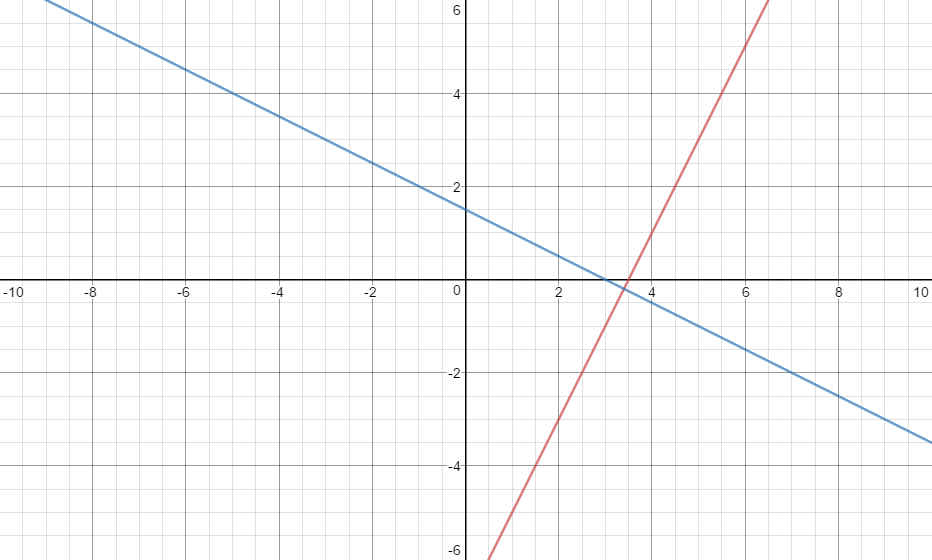
What could be the equation of a line that is perpendicular to `2x-y=7`?

Answer 1

When given an equation of a line, `ax + by = c`, you can make a perpendicular line by swapping "a" and "b" and then changing the sign of one of them.

Explanation:

Given: `2x - y = 7`

Matching given equation with the variables, `a = 2 and b = -1`.

Swap "a" and "b"

-x + 2y = 7

Because b is negative, let's change that one:

x + 2y = 7

Is perpendicular to `2x - y = 7`. Here is a graph to prove it:

The red line is `2x - y = 7`
The blue line is `x + 2y = 7`

If you want the perpendicular line to go through a given point, then make the constant term on the right a variable (for example k)

`x + 2y = k`

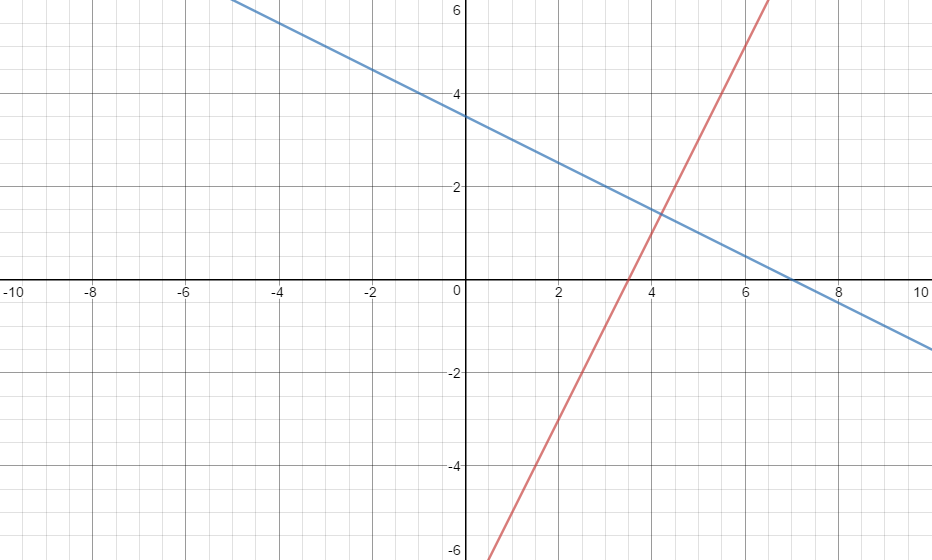
Now lets make the perpendicular line go through the point `(1,1)` by substituting 1 for x, 1 for y and the solving for k:

`1 + 2(1) = k`

`k = 3`

The equation of the line that perpendicular to `2x - y=7` and goes through the point `(1,1)` is:

`x + 2y = 3`

Here is a graph to prove it: