Question

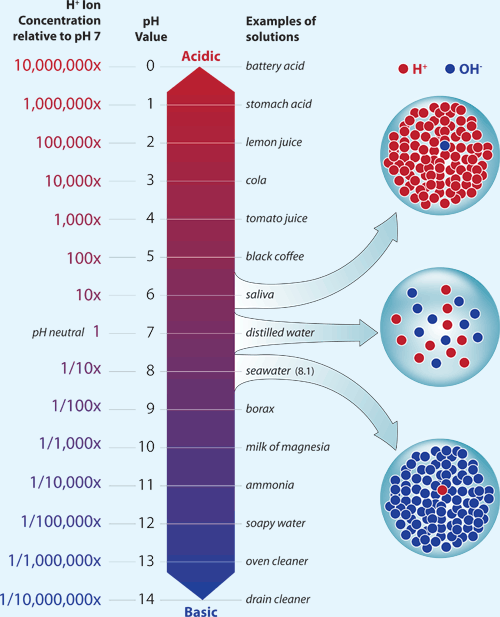
What does it mean if a solution has a pH of 6.0?

Answer 1

That it contains `10` times more hydronium cations than a neutral solution at room temperature.

Explanation:

As you know, the `"pH"` of a solution is a measure of the concentration of hydronium cations, `"H"_3"O"^(+)`, present in this solution.

More specifically, to find the `"pH"` of a solution, you need to take the negative log base `10` of the concentration of hydronium cations.

`"pH" = - log(["H"_3"O"^(+)])`

You can rewrite this equation as

`["H"_3"O"^(+)] = 10^(-"pH")`

Now, pure water at room temperature has

`"pH" = 7`

This implies that the concentration of hydronium cations in pure water at room temperature is equal to

`["H"_3"O"^(+)] = 10^(-7)color(white)(.)"M"`

`["H"_3"O"^(+)] = 1 * 10^(-7)color(white)(.)"M"`

In order for the `"pH"` of the solution to decrease by `1` unit, the concentration of hydronium cations must increase by an order of magnitude, i.e. `10`-fold.

So for `"pH" = 6.0`, you have

`["H"_3"O"^(+)] = 10^(-6.0)color(white)(.)"M"`

`["H"_3"O"^(+)] = 1 * 10^(-6)color(white)(.)"M"`

This corresponds to an increase by an order of magnitude in the concentration of hydronium cations, since

`(["H"_ 3"O"^(+)]_ "pH = 6.0")/(["H"_ 3"O"^(+)]_ "pH = 7") = (1 * 10^(-6)color(red)(cancel(color(black)("M"))))/(1 * 10^(-7)color(red)(cancel(color(black)("M")))) = 10`

You can thus say a solution that has a `"pH"` equal to `6.0` contains `10` times more hydronium cations than a solution that has `"pH" = 7`, i.e. than a neutral solution at room temperature.

This, of course, implies that you are dealing with a solution that is slightly acidic, since that is what `"pH" < 7` at room temperature implies.