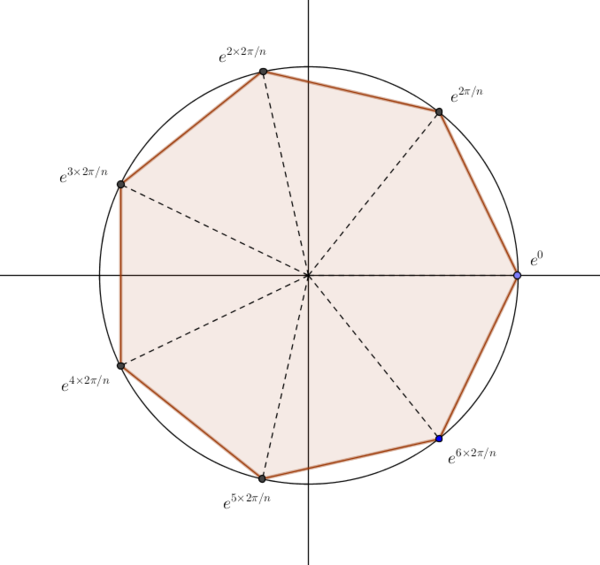
What does the graph of the seventh root of unity look like on a unit circle like the one in the pictured attached?
2 Answers
There are seven seventh roots of unity,
Explanation:
Euler's Identity to an even integer power of
Now we see
That's seven distinct seventh roots, given by any seven consecutive
Another view
See below
Explanation:
It is interesting to note that the
The 7 roots of