Question

What does v=dx/dt means?

Answer 1

It represents the instantaneous variation of POSITION with TIME. also known, as velocity.

Explanation:

The explanation can be a little bit boring but...
Cosider a car that moves from position `x_1` at instant `t_1` to position `x_2` at instant `t_2`.
You can represent the variation of position using a number (a kind of position parameter) called average velocity as:
`v_(av)=(x_2-x_1)/(t_2-t_1)=(Deltax)/(Deltat)`

The problem is: "what happened in the middle? Did the car stop...go faster...slower...?"

To "look" inside your interval you can reduce the time interval and try to focus on a specific instant.

This means reducing `Deltat` to zero or at least tend to zero!

So, basically, you'll be able to evaluate the velocity at a point (not interval) and have an instantaneous velocity!

It is easy to say but mathematically...you need:
`v_("inst")=lim_(Deltat->0)(Deltax)/(Deltat)=(dx)/(dt)` which is the "symbol" for an operation done on a function called Derivative.

For example:
consider a car that has a position modelled by the function:
`x(t)=-4t^2+3t-2` (I invented it)
So
instantaneous velocity will be given as:
`(dx)/(dt)=-8t+3`
So at each instant you will get the velocity at exactly that instant: for example at `t=0` `v_("inst")=-8*0+3=3m/s`

Hope it is not too confusing!

Answer 2

`v = (dx)/(dt)`

This means that the velocity over a certain period of time is the instantaneous change in position `(dx)` over the instantaneous change in time `(dt)`. This period of time is intentionally very small, hence "instantaneous".

Imagine looking at a graph of position (x) vs. time (t) and determining the slope of that graph.

`(dx)/(dt) = (Deltax)/(Deltat)`

...when the change, `Delta`, is very, very small. You are essentially zooming into the graph until it looks linear (try it on your calculator on, let's say, `y = sqrtx`).

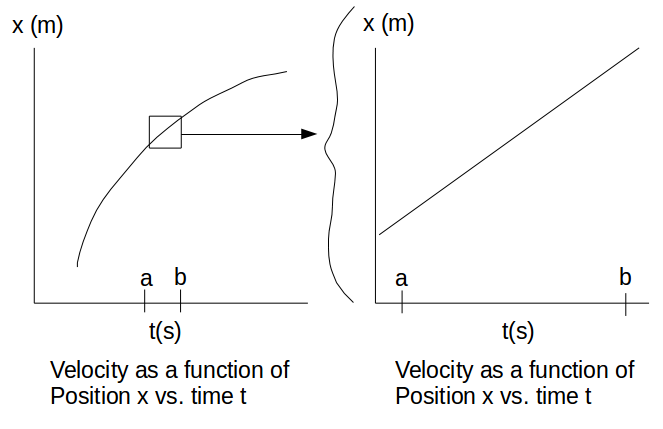
The little square represents what you see on your calculator.

When that is the case, you can take two points very, very close to each other, like `"1.003 s"` and `"1.006 s"` for example, calculate the slope using `(x_2 - x_1)/(t_2 - t_1)`, and you have the velocity at about `"1.0045 s"` in `"m/s"` (halfway between the two times).

You can also shift this small square window around and find velocities at other points on the same curve in a similar fashion, and they would be instantaneous velocities, at instantaneous moments in time.