What expression represents the #DeltaH# for a chemical reaction in terms of the potential energy, #E#, of its products and reactants?
1 Answer
There isn't one I can think of off-hand, so we'll have to derive it. I get:
#barul(|" "stackrel(" ")(DeltaH_(rxn) = DeltaE_(rxn) + PDeltaV_(rxn))" "|)#
Consider a general potential energy diagram for an endothermic reaction
#A + B -> C + D# ,
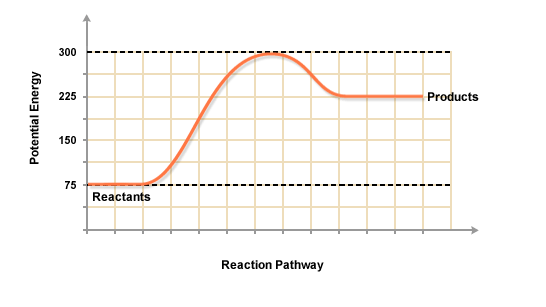
Let the reactants
#DeltaE_(rxn) = (E_C + E_D) - (E_A + E_B)#
So, if we know the ground-state energies of the reactants and products, we can calculate
From the Maxwell Relation for the enthalpy
#dH = TdS + VdP#
Now, consider adding and subtracting reversible pressure-volume work
#dH = TdS - PdV + PdV + VdP#
The first two terms are given in the first law of thermodynamics, i.e. conservation of energy for a reversible process in a thermodynamically-closed system:
#dE = q_(rev) + w_(rev) = TdS - PdV# ,where
#q_(rev)# is the reversible heat flow and#S# is the entropy.
Thus, we can rewrite this as:
#dH = dE + PdV + VdP#
Now, in ordinary reactions, we are at a constant atmospheric pressure, so
#dH = dE + PdV#
By integrating this from an initial state to a final state, we obtain:
#DeltaH = DeltaE + PDeltaV# ,
which should be familiar from general chemistry. For a reaction, we can write this as:
#color(blue)(barul(|" "stackrel(" ")(DeltaH_(rxn) = DeltaE_(rxn) + PDeltaV_(rxn))" "|))#
Thus, if we also know the pressure and the change in volume (through knowing the masses and the densities of each substance), we can then calculate

