What is 4-x^2+x^4 divided by x^2+x+5?
1 Answer
Jul 27, 2018
Explanation:
(4-x^2+x^4)/(x^2+x+5)
= (x^4-x^2+4)/(x^2+x+5)
= (x^4+x^3+5x^2-x^3-6x^2+4)/(x^2+x+5)
= (x^2(x^2+x+5)-x^3-6x^2+4)/(x^2+x+5)
= x^2+(-x^3-6x^2+4)/(x^2+x+5)
= x^2+(-x^3-x^2-5x-5x^2+5x+4)/(x^2+x+5)
= x^2+(-x(x^2+x+5)-5x^2+5x+4)/(x^2+x+5)
= x^2-x+(-5x^2+5x+4)/(x^2+x+5)
= x^2-x+(-5x^2-5x-25+10x+29)/(x^2+x+5)
= x^2-x+(-5(x^2+x+5)+10x+29)/(x^2+x+5)
= x^2-x-5+(10x+29)/(x^2+x+5)
Alternatively, we can find the same result by long dividing tuples representing the coefficients of the powers of
In our example, we want to divide "
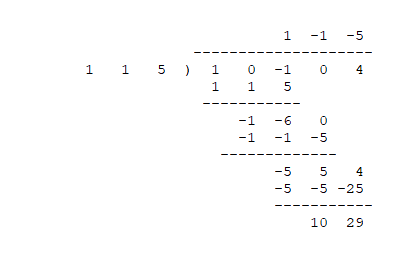
So

