When scaling a plane around a point, the result is a plane of a different size but the same shape.
It is highly-recommended to draw everything out.
SCALING FROM A CENTERPOINT
Scaling is commonly done about #(0,0)#, in which case it looks like this:
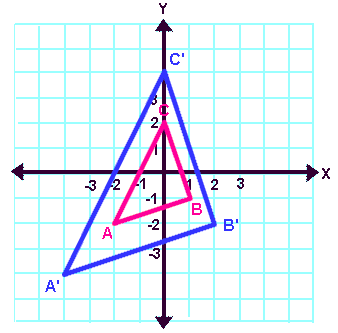
and you can see that the #z#-axis (into/out of the screen, or in the #hatk# direction) would pass through the exact centers of both triangles #DeltaABC# and #DeltaA'B'C'#.
In this scenario, it is clearer what has happened to each point. #A("-2,-2")# has been scaled outwards by a factor of #2# to achieve #A'("-4,-4")#, #B("1,1")# has been scaled outwards by a factor of #2# to achieve #B'("2,2")#, and #C("0,2")# has been scaled outwards by a factor of #2# to achieve #C'("0,4")#.
In general, scaling about a central point is given as:
#color(blue)(P'(x,y) = P(kx,ky) " where " k in RR " and " k > 0)#
SCALING OFF-CENTER
Scaling might also be done from an arbitrary non-central point. For instance, scaling a triangular plane #D_k# outwards from point #O# by non-zero scalar #k in RR# where #k = (OA')/(OA) = (OB')/(OB) = (OC')/(OC)# gives the transformation
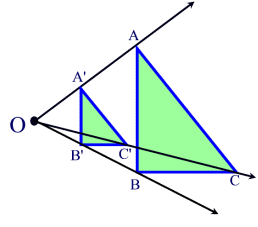
for which #A#, #B#, and #C# were points on the green triangle. In this case, the scaling shrunk #DeltaABC# into #DeltaA'B'C'# by a factor of #k# where #0 < k < 1#.
You can see that #DeltaABC# and #DeltaA'B'C'# expand along the axes that pass through points #O#, as well as #A#, #B#, #C#, #A'#, #B'#, or #C'#.



