What is an equilibrium solution to a differential equation?
2 Answers
I assume you mean the steady-state solution to a partial differential equation. For example, consider the heat equation for a 1D uniform rod of finite length
#(delu)/(delt) = k(del^2u)/(delx^2)# where
#k# is a constant.
For a (thermal) equilibrium problem, assume that the change in temperature is zero, i.e.
#0 = k(del^2u)/(delx^2) = (del^2u)/(delx^2)#
Thus, the change in temperature across the rod is linear, i.e. you have a linear temperature gradient:
#int int ((del^2u)/(delx^2))dx^2#
#= (d^2)/(dx^2)int int udx^2#
(Leibniz's rule)
#= u = int c_1dx#
#= c_1x + c_2#
For instance, let's say you had the two Dirichlet boundary conditions:
#u(0,t) = 0#
#u(L,t) = T#
Then you would have from the first boundary condition:
#c_1(0) + c_2 = 0#
#=> c_2 = 0#
Thus:
#c_1L = T# from the second boundary condition, and:
#=> c_1 = T/L#
and we'd have:
#color(blue)(u(x) = (T/L)x)#
An equilibrium solution is a solution to a DE whose derivative is zero everywhere. On a graph an equilibrium solution looks like a horizontal line.
Given a slope field, you can find equilibrium solutions by finding everywhere a horizontal line fits into the slope field. Equilibrium solutions come in two flavours: stable and unstable. These terms are easiest to understand by looking at slope fields.
A stable equilibrium solution is one that other solutions are trying to get to. If we pick a point a little bit off the equilibrium in either direction, the solution that goes through that point tries to snuggle up to the equilibrium solution.
An unstable equilibrium solution is one that the other solutions are trying to get away from. If we pick a point a little bit off the equilibrium, the solution that goes through that point is trying to run away from the equilibrium solution.
Example:
Consider the DE;
#y'=(y^2-4)(y+1)^2#
If we have
Here is the sketch of the integral curves.
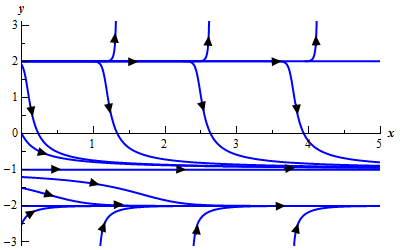
From this it is clear (hopefully) that
In cases where solutions on one side of an equilibrium solution move towards the equilibrium solution and on the other side of the equilibrium solution move away from it we call the equilibrium solution semi-stable, and


