if #x=2#, then #x-2 = 0#
if #x=5#, then #x-5 = 0#
dividing by #0# is an undefined result, so there are vertical asymptotes at these #x#-values.
the graph #1/x# has a horizontal asymptote at #y=0#, since #0# can only be a result of division when the numerator is #0#.
this means that putting the numbers #(x-2)# and #(x-5)# in the denominator forms asymptotes when #x-2=0# or #x-5=0#, or when #x=2#, #x=5#.
adding #3# raises the asymptote to #y = 3#.
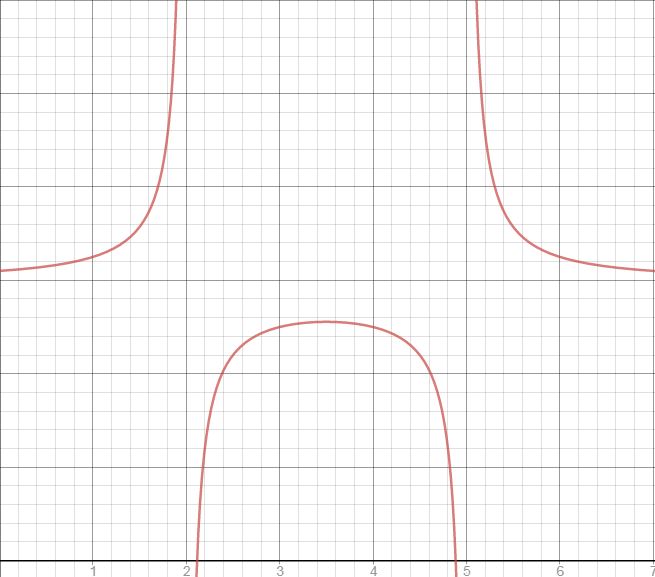
a section of the graph, where:
the #y#-values on either side decrease but always stay above #3#
(the point #(x,3)# does not exist on this graph)
as #x#-values go towards (tend to) #2#, #y# either goes infinitely upwards or infinitely downwards, depending on whether it tends to #2# from below or above. neither side has a point #(2,y)#.
the same is true for the other vertical asymptote, #x=5#.

