What is #B# in the equation #sin B = .7547#?

1 Answer
Sridhar V.
May 6, 2018

#" "#
#color(blue)(B~~48.9^@#

Explanation:

#" "#
Given: #color(red)(Sin(B)=0.7547)#

View the #sin(x)# graph both in Radians and in Degree mode:

#Sin(x)# in Radians Mode:

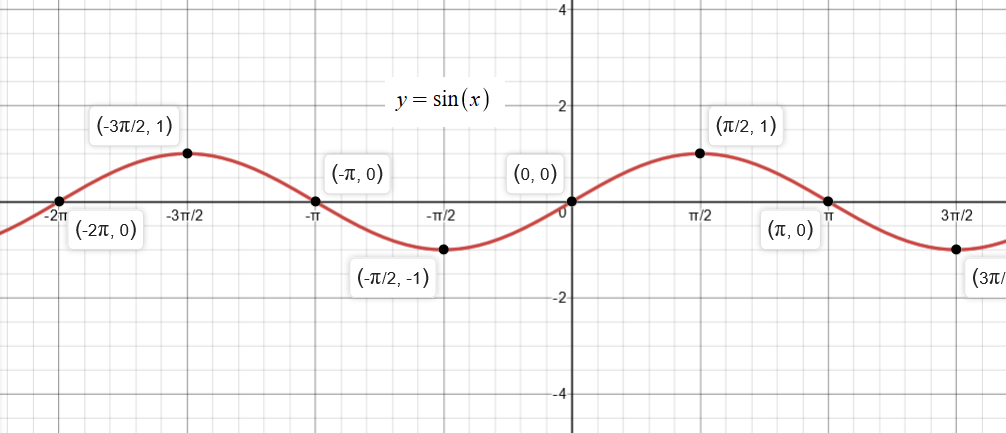
enter image source here

#Sin(x)# in Degree Mode:

enter image source here

The Range of the Sin(x) function is between #color(red)((+1)# and #color(red)((-1)#, the maximum and the minimum points of the graph and these values lie on the y-axis.

Find the value of #color(red)(B#, using the #ArcSin# function, which is the Inverse of Sin function.

If #sin(B)=0.7547#, then #B=sin^-1(0.7547)#

Using a calculator, #B~~ 48.999^@#

Hence,

#color(blue)(B~~48.9^@#

Hope it helps.

Related questions
Impact of this question
2700 views around the world
You can reuse this answer
Creative Commons License