The following cell is operated as an electrolytic cell, using a current of 0.480 A . The volume of each solution is 100.0 mL. Electrolysis is stopped after 10.00 h , and the cell is allowed to function as a voltaic cell. What is #E_(cell)# at this point?
Exercise 20.87
The following cell is operated as an electrolytic cell, using a current of 0.480 A . Assume that the volume of each solution is 100.0 mL. Electrolysis is stopped after 10.00 h , and the cell is allowed to function as a voltaic cell.
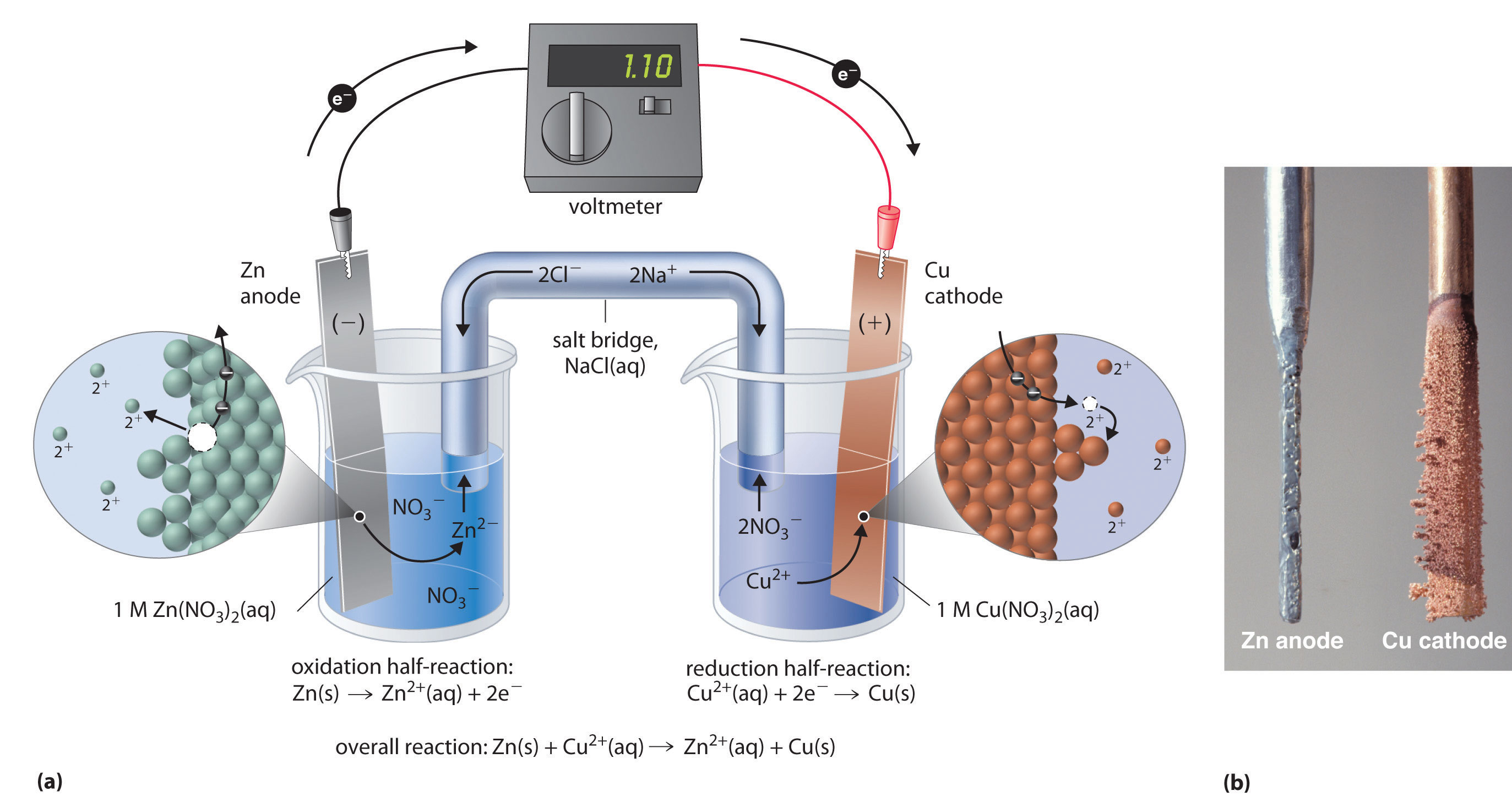
#Zn(s)|Zn(NO_3)_2(1.00M)||Cu(NO_3)_2(1.00M)|Cu(s)#
Exercise 20.87
The following cell is operated as an electrolytic cell, using a current of 0.480 A . Assume that the volume of each solution is 100.0 mL. Electrolysis is stopped after 10.00 h , and the cell is allowed to function as a voltaic cell.
1 Answer
Explanation:
!! EXTREMELY LONG ANSWER !!
Let's start by calculating
You know that you have
The balanced chemical equation that describes this redox reaction looks like this
#"Zn"_ ((s)) + "Cu"_ ((aq))^(2+) -> "Zn"_ ((aq))^(2+) + "Cu"_ ((s))#
Write down the reduction half-reactions and the standard reduction potentials for zinc and for copper
#"Zn"_ ((aq))^(2+) + 2"e"^(-) -> "Zn"_ ((s))" "E_"red"^@ = - "0.763 V"#
#"Cu"_ ((aq))^(2+) + 2"e"^(-) -> "Cu"_ ((s))" "E_"red"^@ = + "0.337 V"#
http://www.chemeddl.org/services/moodle/media/QBank/GenChem/Tables/EStandardTable.htm
Now, notice that zinc is being oxidized to zinc cations at the anode, so reverse the reduction half-reaction for zinc to get the oxidation half-reaction
#"Zn"_ ((s)) -> "Zn"_ ((aq))^(2+) + 2"e"^(-)" "E_"oxi"^@ = - (-"0.763 V")#
You will have
#E_"oxi"^@ = - E_"red"^@#
#E_"oxi"^@ = - (-"0.763 V") = + "0.763 V"#
The standard cell potential is equal to
#E_"cell"^@ = E_"red"^@ + E_"oxi"^@#
In your case, this will be equal to
#E_"cell"^@ = +"0.337 V" + "0.763 V" = +"1.100 V"#
Keep this in mind because it will come in handy later.
Since you have
In other words, when the cell is operating as a voltaic cell, you can expect the mass of the zinc electrode to decrease and the mass of the copper electrode to increase.
Now, you're operating this cell as an electrolytic cell. This means that you're using an external power source to force the reverse reaction to take place
#"Cu"_ ((s)) + "Zn"_ ((aq))^(2+) -> "Cu"_ ((aq))^(2+) + "Zn"_ ((s))#
In this case, copper metal is being oxidized to copper(II) cations, so you should expect the mass of the anode to decrease and the concentration of copper(II) cations to increase.
Zinc cations are being reduced to zinc metal, so you should expect the mass of the cathode to increase and the concentration of zinc cations to decrease.
So, you know that you're using a current of
As you know, you have
#"1 A" = "1 C"/"1 s"#
Your current delivers
#10.00 color(red)(cancel(color(black)("h"))) * (3600 color(red)(cancel(color(black)("s"))))/(1color(red)(cancel(color(black)("h")))) * "0.480 C"/(1color(red)(cancel(color(black)("s")))) = 1.728 * 10^4# #"C"#
Now,
#1.728 * 10^4 color(red)(cancel(color(black)("C"))) * "1 mole e"^(-)/(9.65 * 10^4color(red)(cancel(color(black)("C")))) = "0.1791 moles e"^(-)#
You have
#"Cu"_ ((s)) -> "Cu"_ ((aq))^(2+) + 2"e"^(-)#
Since
#0.1791 color(red)(cancel(color(black)("moles e"^(-)))) * "1 mole Cu"^(2+)/(2color(red)(cancel(color(black)("moles e"^(-))))) = "0.08955 moles Cu"^(2+)#
Similarly, you have
#"Zn"_ ((aq))^(2+) + 2"e"^(-) -> "Zn"_ ((s))#
This time, you consume
#0.1791 color(red)(cancel(color(black)("moles e"^(-)))) * "1 mole Zn"^(2+)/(2color(red)(cancel(color(black)("moles e"^(-))))) = "0.08955 moles Zn"^(2+)#
Use the molarities and the volumes of the two half-cells to calculate the initial number of moles of each cation
#100.0 color(red)(cancel(color(black)("mL"))) * "1.00 moles Cu"^(2+)/(10^3color(red)(cancel(color(black)("mL")))) = "0.100 moles Cu"^(2+)#
#100.0 color(red)(cancel(color(black)("mL"))) * "1.00 moles Zn"^(2+)/(10^3color(red)(cancel(color(black)("mL")))) = "0.100 moles Zn"^(2+)#
After you disconnect the power source, the resulting solutions will contain
#n_ ("Cu"^(2+)) = "0.100 moles" + "0.08955 moles" = "0.1896 moles Cu"^(2+)#
#n_ ("Zn"^(2+)) = "0.100 moles" - "0.08955 moles" = "0.01045 moles Cn"^(2+)#
Calculate the new concentrations of the two cations
#["Cu"^(2+)] = "0.1896 moles"/(100.0 * 10^3"L") = "1.896 M"#
#["Zn"^(2+)] = "0.01045 moles"/(100.0 * 10^3"L") = "0.1045 M"#
At this point, you allow the cell to function as a voltaic cell. You're no longer under standard conditions because the concentrations of the two solutions have changed, so you must calculate the cell potential using--you can assume that the temperature does not change, i.e. you're still working at
#E_"cell" = E_"cell"^@ - 0.0592/n * log(Q)#
Here
#n# is the number of moles of electrons transferred in the redox reaction#Q# is the reaction quotient
Keep in mind that the cell is working as a voltaic cell again, so you have
#"Zn"_ ((s)) + "Cu"_ ((aq))^(2+) -> "Zn"_ ((aq))^(2+) + "Cu"_ ((s))#
The reaction quotient is equal to
#Q = (["Zn"^(2+)])/(["Cu"^(2+)])#
The number of moles of electrons transferred in the balanced redox reaction will be equal to
#E_"cell" = E_"cell"^@ - 0.0592/2 * log((["Zn"^(2+)])/(["Cu"^(2+)]))#
This will get you
#E_"cell" = +"1.100 V" - 0.0592/2 * log( (0.1045 color(red)(cancel(color(black)("M"))))/(1.896 color(red)(cancel(color(black)("M")))))#
#color(darkgreen)(ul(color(black)(E_"cell" = +"1.14 V")))#
The answer is rounded to three sig figs, the number of sig figs you have for the current.

