What is exact change in position of the particle?

Question

The velocity of a particle moving along the x-axis is given by #f(t)=15−5t#cm/s. Use a graph of f(t) to find the exact change in position of the particle from time t=0 to t=4 seconds.

4836 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-11T06:13:43

Change in position is also called displacement. It is a vector quantity.

Given #f(t)=15-5t#

at #t=0#, #f=15#
at #t=1#, #f=10#
at #t=2#, #f=5#
at #t=3#, #f=0#
at #t=4#, #f=-5#

Plot graph as below
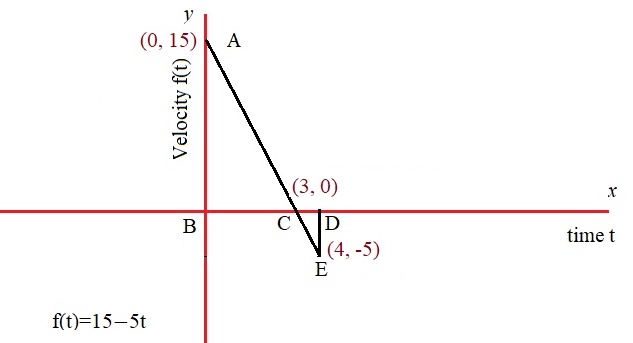
my comp
#"Displacement"="Area under the curve for "t=0 to t=4#

We know that #"Area of a triangle "=1/2xx"base"xx"height"#

#:. "Displacement"="Area of "Delta ABC+"Area of "Delta CDE#
#=> "Displacement"=1/2xx3xx15+1/2xx(-5)xx1#
#=> "Displacement"=22.5-2.5=20cm#