What is meant by a stress on a reaction at equilibrium?

1 Answer
Doc048
May 8, 2017

There are three 'Stress Factors' that affect the stability of an equilibrium:
1. Concentration Effects
2. Temperature Effects
3. Pressure-Volume Effects

Explanation:

Kinda long, but I had JPEGs in my files => Don't mind sharing.

A system (Reaction) at equilibrium is producing products as fast as it is producing reactants. This is known as the Law of Mass Action. That is ...

Rate of forward reaction = Rate of reverse reaction

When this condition exists, the reaction system is said to be in a 'stable' Dynamic Equilibrium'. While the concentrations of reactants and products appear to be constant, the chemical or physical process is still taking place.

To visualize this, think of the equilibrium process as being balanced on a See-Saw. Such as ...
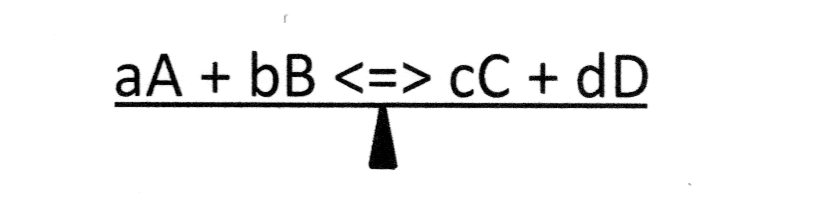
enter image source here
If a stress is applied, the balance will be disturbed and the See-Saw will tilt toward the side of the equation to which the stress factor is applied.

The reaction will then shift away from the applied stress and establish a 'new' equilibrium with different concentration values for the reactants and products. => LeChatelier's Principle

Consider Concentration Effects:
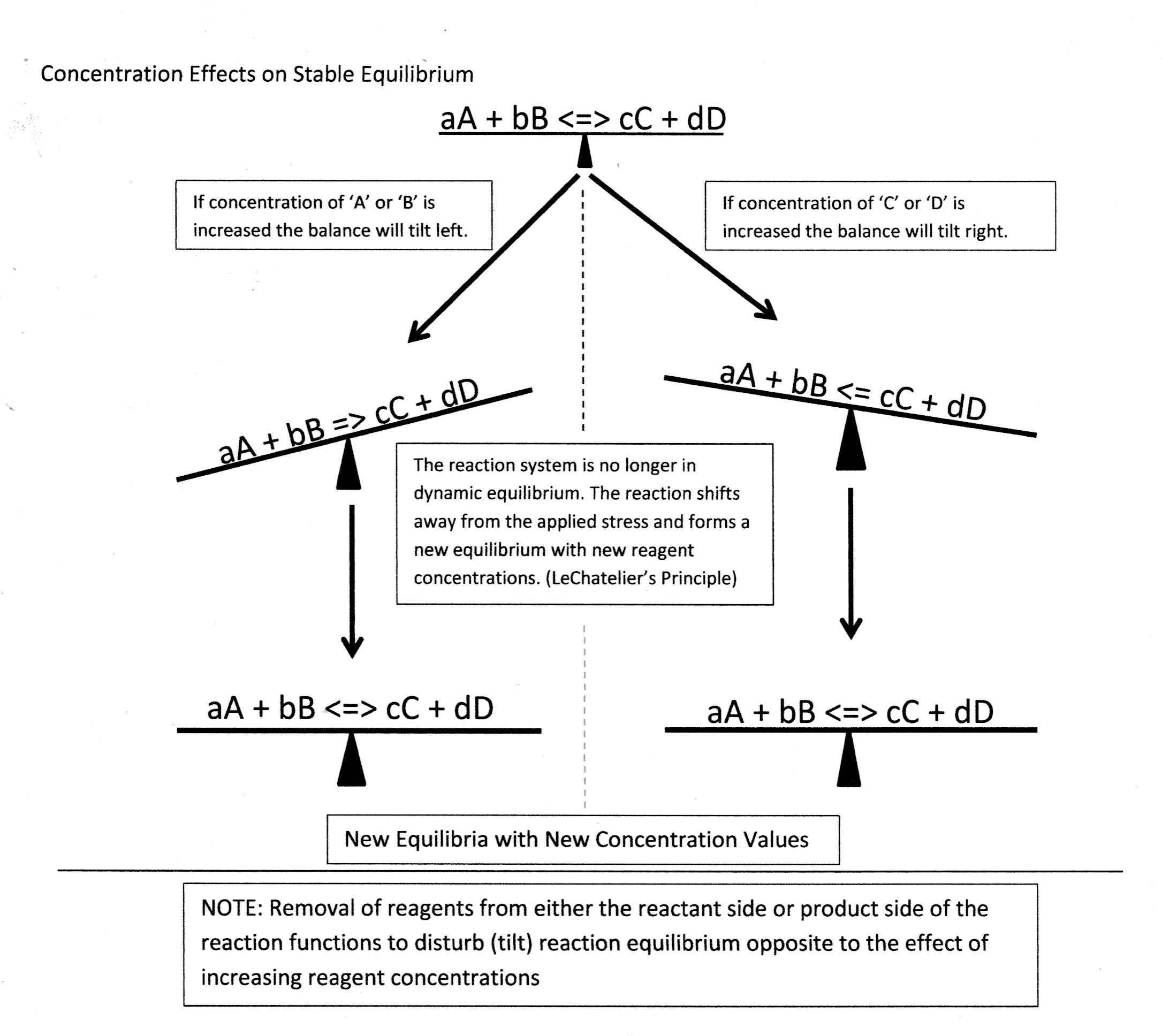
enter image source here
Concept Check:
Consider the Rxn:
#FeO(s)# + #CO(g)# #-># #Fe^o(s)#+#CO_2(g)#
Stress Factor => Removing #CO(g)# (lighter reactant side) => Right tilt => Rxn Shifts Left to to establish new equilibrium.

Consider the Rxn:
#COCl_2(g) -> CO(g) + Cl_2(g)#
Stress Factor => Adding #Cl_2(g)# into the equilibrium mixture => (heavier product side) => Rxn balance tilts right => Rxn Shifts Left to to establish new equilibrium.

Stress Factor => removing #Cl_2(g)# from the from the equilibrium mixture => (Lighter Product Side) => Rxn balance would tilt Left => Rxn Shifts Right to establish new equilibrium.

Consider Temperature Effects:
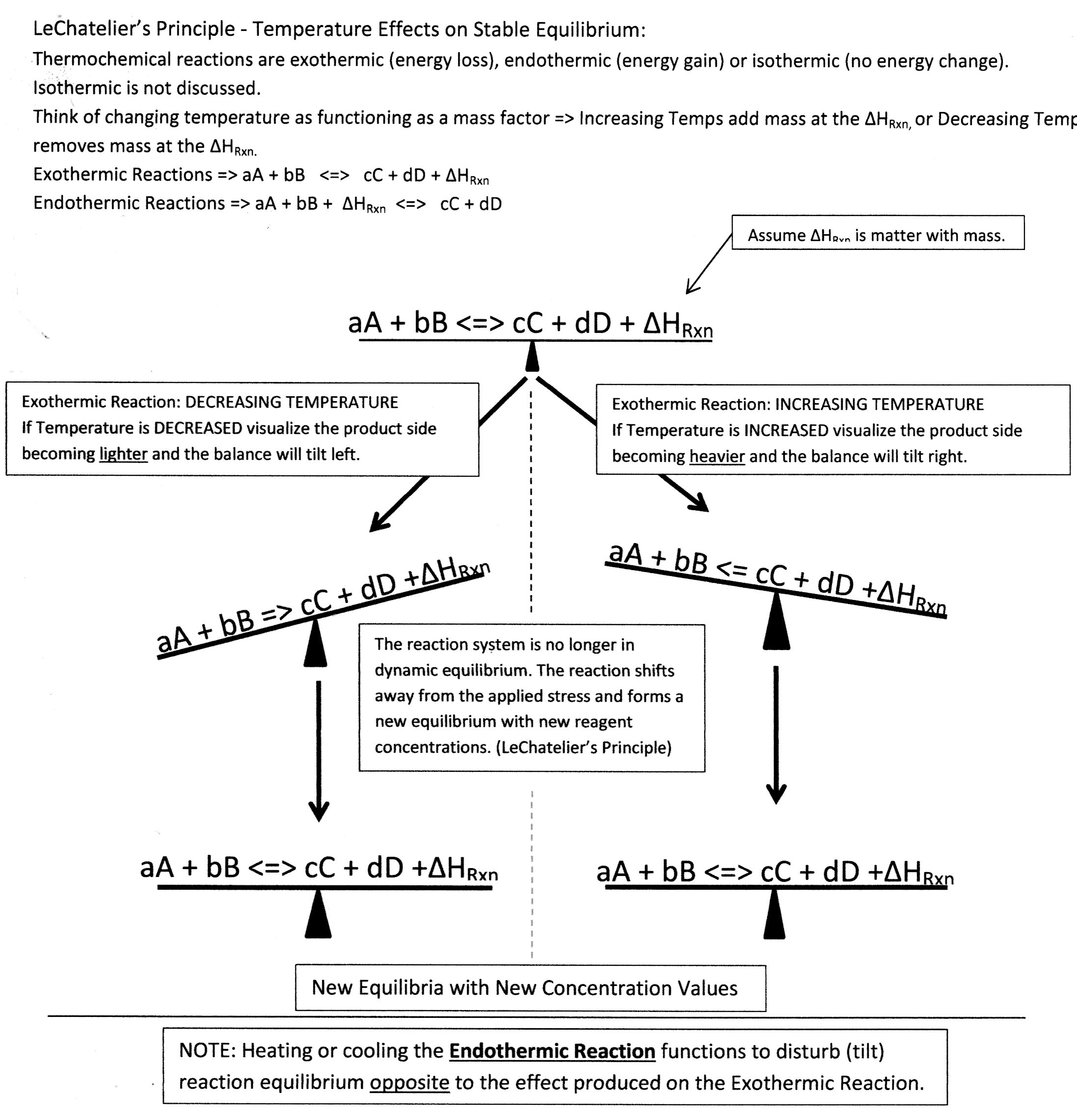
enter image source here

Concept Check:
Consider the reaction:
#CO(g)# + #2H_2(g)# -> #CH_3OH(G)# + 21.7Kj
Stress Factor => Cooling rxn environment => product side is lighter => Rxn balance would tilt left => Rxn Shifts Right to establish new equilibrium.

Consider the reaction:
#2H_2O# + 484Kj -> #2H_2(g)#+#O_2(g)#
To increase decomposition => Stress Factor => Increase temperature around reaction environment => Rxn balance would tilt left => Rxn Shifts Right to establish new equilibrium.

Consider Pressure-Volume Effects:
enter image source here
Concept Check: Increasing pressure will ...
#2H_2(g)# + #O_2(g)# #-># #2H_2O(g)# => Shifts Right

#2H_2O(g)# -> #2H_2O(l)# => Shifts Right [#V_"m" H_"2"O(l) = 0#]

#CH_4(g)#+#2O_2(g)# -> #CO_2(g)#+#2H_2O(l)# => Shifts Right (P-V Effects apply to gas phase components only)

Same Rxn but note => all gas phase components.
#CH_4(g)#+#2O_2(g)# -> #CO_2(g)#+#2H_2O(g)# => No Shift Occurs
#sum(V_m)(Reactants)# = #sum(V_m)(Products)#

Related questions
See all questions in Dynamic Equilibrium
Impact of this question
12511 views around the world
You can reuse this answer
Creative Commons License