What is the angle between #<-1,8,6 ># and #< -6,3,0>#?

1 Answer
Morgan
Dec 31, 2016

#theta~~63.58^o#

Explanation:

The equation for the angle between two vectors is given by:

#cos(theta)=(veca*vecb)/(|veca|*|vecb|)#

Where #veca=< -1,8,6 ># and #vecb= < -6,3,0 >#

First we find the dot product of the two vectotrs:

#veca*vecb= < -1,8,6 > *< -6,3,0 >#

#=>(-1*-6)+(8*3)+(6*0)#

#=>6+24=30#

Next, we find the product of the magnitude of each vector:

#|veca|=sqrt((a_x)^2+(a_y)^2+(a_z)^2)#

#=>sqrt((-1)^2+(8)^2+(6)^2)#

#=>sqrt(1+64+36)#

#=>sqrt(101)#

#|vecb|=sqrt((b_x)^2+(b_y)^2+(b_z)^2)#

#=>sqrt((-6)^2+(3)^2+(0)^2)#

#=>sqrt(36+9+0)#

#=>sqrt(45)#

And #sqrt(45)*sqrt(101)=sqrt(4545)#

Revisiting our original equation, we can solve for #theta# by taking the inverse cosine:

#theta=cos^-1((veca*vecb)/(|veca|*|vecb|))#

Substituting in our values found above:

#theta=cos^-1((veca*vecb)/(|veca|*|vecb|))#

#=>theta=cos^-1((30)/(sqrt(4545)))#

This comes out to #~~63.58^o# or #~~1.11rad#

Explanation of equation:

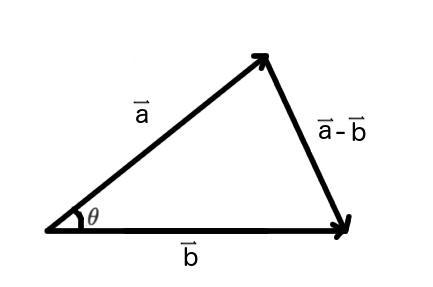
We can derive the given equation using a geometric interpretation of the vectors.

Given vectors #veca# and #vecb#:

enter image source here

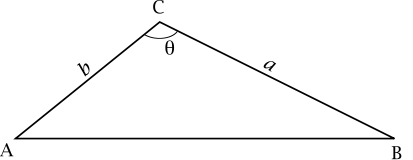
By the law of cosines, given:

wiki

#c^2=a^2+b^2-2abcos(theta)#

Applying this to our vector-made triangle:

#|veca-vecb|^2=|veca|^2+|vecb|^2-2|veca|*|vecb|cos(theta)#

Simplifying:

#=>(veca-vecb)*(veca-vecb)=(veca*veca)+(vecb*vecb)-2|veca|*vec|b|cos(theta)#

#=>cancel(veca^2)-2(veca*vecb)cancel(+vecb^2)=cancel(veca^2)+cancel(vecb^2)-2|veca|*vec|b|cos(theta)#

#=>-2(veca*vecb)=-2|veca|*vec|b|cos(theta)#

#=>(veca*vecb)=|veca|*vec|b|cos(theta)#

Solve for #cos(theta)#:

#=>cos(theta)=(veca*vecb)/(|veca|*vec|b|)#

Related questions
See all questions in Vectors
Impact of this question
1649 views around the world
You can reuse this answer
Creative Commons License