Question

What is the angle between `<5,1,4 >` and `< 3,1,9 >`?

Answer 1

`32.7 °`(3sf)

Explanation:

The angle `theta` between two vectors `vec A` and `vec B` is related to the modulus (or magnitude) and scaler (or dot) product of `vec A` and `vec B` by the relationship:

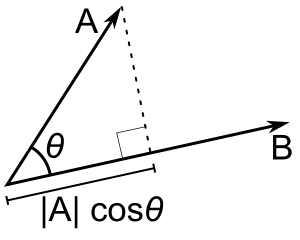
`vec A * vec B = |A| |B| cos theta`

By convention when we refer to the angle between vectors we choose the acute angle.

So for this problem, let the angle betwen `vecu` and `vecv` be `theta` then:

`vec u=<<5,1,4>>` and `vec v=<<3,1,9>>`

The modulus is given by;

`|vec u| = |<<5,1,4>>| = sqrt(5^2+1^2+4^2)=sqrt(25+1+16)=sqrt(42)`
`|vec v| = |<<3,1,9>>| = sqrt(3^2+1^2+9^2)=sqrt(9+1+81)=sqrt(91)`

And the scaler product is:

`vec u * vec v = <<5,1,4>> * <<3,1,9>>`
`\ \ \ \ \ \ \ \ \ \ = (5)(3) + (1)(1) +(4)(9)`
`\ \ \ \ \ \ \ \ \ \ = 15+1+36`
`\ \ \ \ \ \ \ \ \ \ = 52`

And so using `vec A * vec B = |A| |B| cos theta` we have:

`52 = sqrt(42) * sqrt(91) * cos theta`
`:. cos theta = (52)/(sqrt(42) * sqrt(91))`
`:. cos theta = 0.841120 ...`
`:. theta = 32.741412 °`
`:. theta = 32.7 °`(3sf)