What is the angle between #<-8,2,8># and #< 6,-4,5>#?
1 Answer
The angle is
Explanation:
The angle
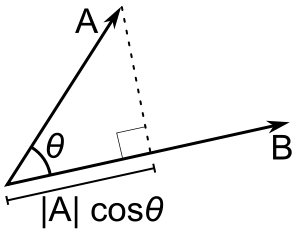
# bb(vec A * vec B) = || bb(vec A) || \ || bb(vec B) || \ cos theta #
By convention when we refer to the angle between vectors we choose the acute angle.
So for this problem, let the angle between
#bb(vec u) = <<-8, 2, 8>>#
#bb(vec v) = <<6, -4, 5>>#
The vector norm is given by;
# | bb(vec u) | = || <<-8, 2, -8 >> || = sqrt(64+4+64)=sqrt(132) #
# | bb(vec v) | = || <<6, -4, 5 >> || = sqrt(36+16+25)=sqrt(77) #
And the scaler (or "dot") product is:
# bb(vec u * vec v) = <<-8, 2, 8>> bb(*) <<6, -4, 5>> #
# \ \ \ \ \ \ \ \ \ \ \ = (-8)(6) + (2)(-4) + (8)(5) #
# \ \ \ \ \ \ \ \ \ \ \ = -48 -8 +40 #
# \ \ \ \ \ \ \ \ \ \ \ = -16 #
And so using
# -16 = sqrt(132)sqrt(77) cos theta #
# :. cos theta = -16/sqrt(10164) #
# " " = -(8sqrt(21))/231 #
# " " =-0.15870392 ... #
# => theta = 99.1316 ... ^o #
This is not acute, so the acute angle between the vectors is:
# theta_("acute") = 180^o - 99.1316 ... ^o #
# " " = 80.8683 ...^o #

