What is the ans please?
3 Answers
The correct answer is
Explanation:
The inequality is
Therefore,
Putting on the same denominator
The correct answer is
Explanation:
given
Subtract
I will use this online graphing calculator to show that the correct answer is A
Explanation:
First I will show you
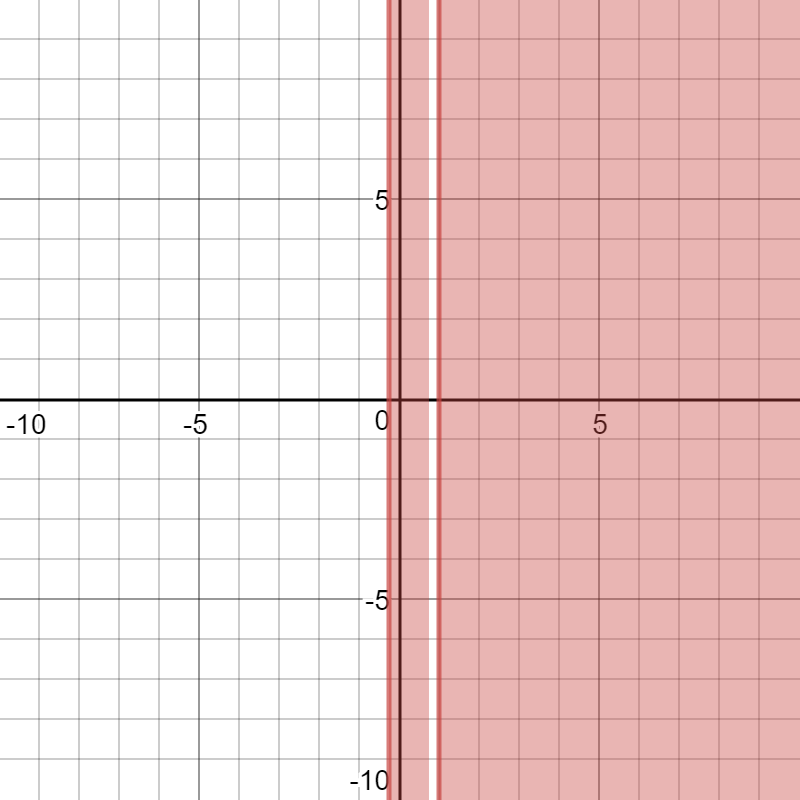
Please observe that it is saying that y is any value that you like but domain of x is
I will save the graph of A for after I have shown that selections B through E are NOT the solutions:
Here is Selection B
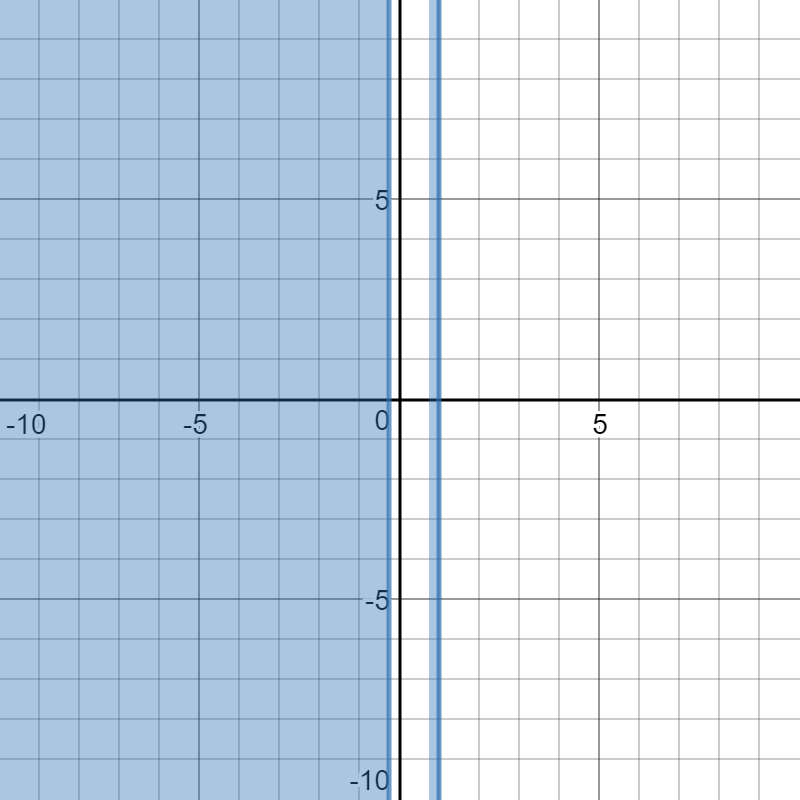
Please observe that it is saying that y is any value that you like but domain of x is
Here is Selection C
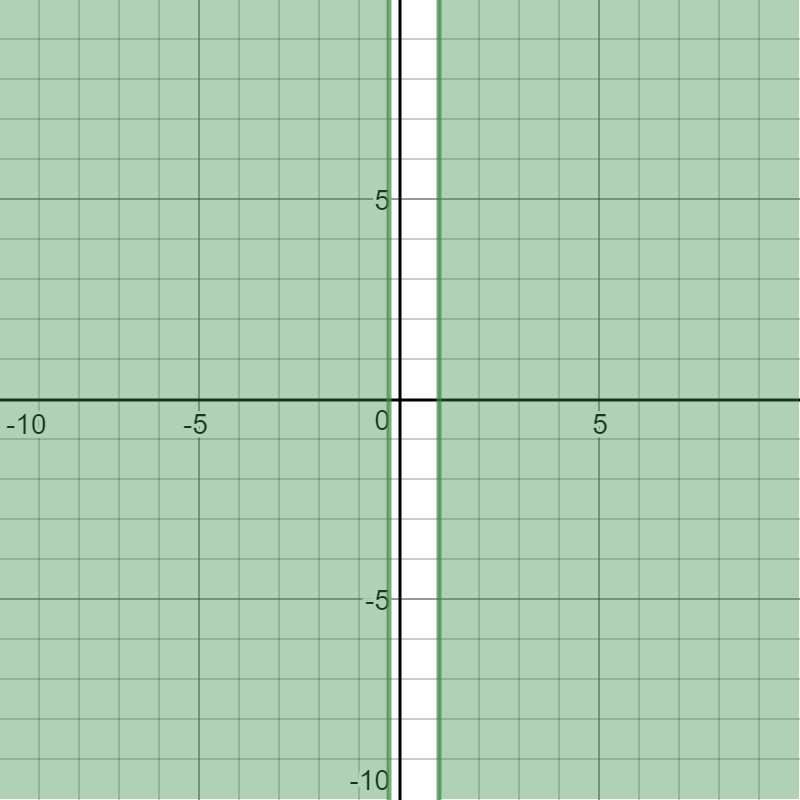
Please observe that it is saying that y is any value that you like but domain of x is
Here is Selection D
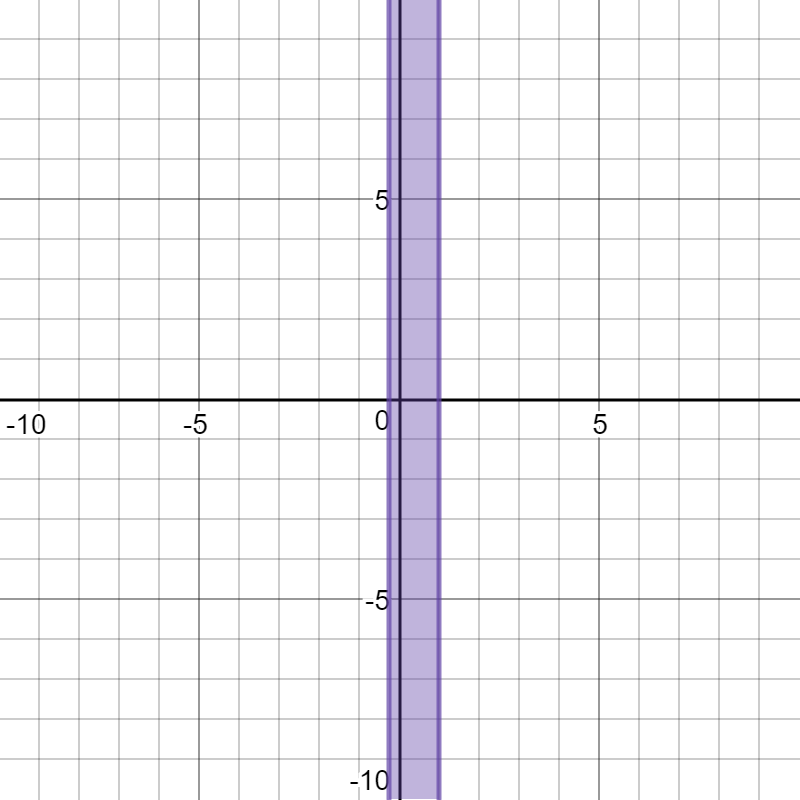
Please observe that it is saying that y is any value that you like but domain of x is
I cannot use the inequality function for selection E
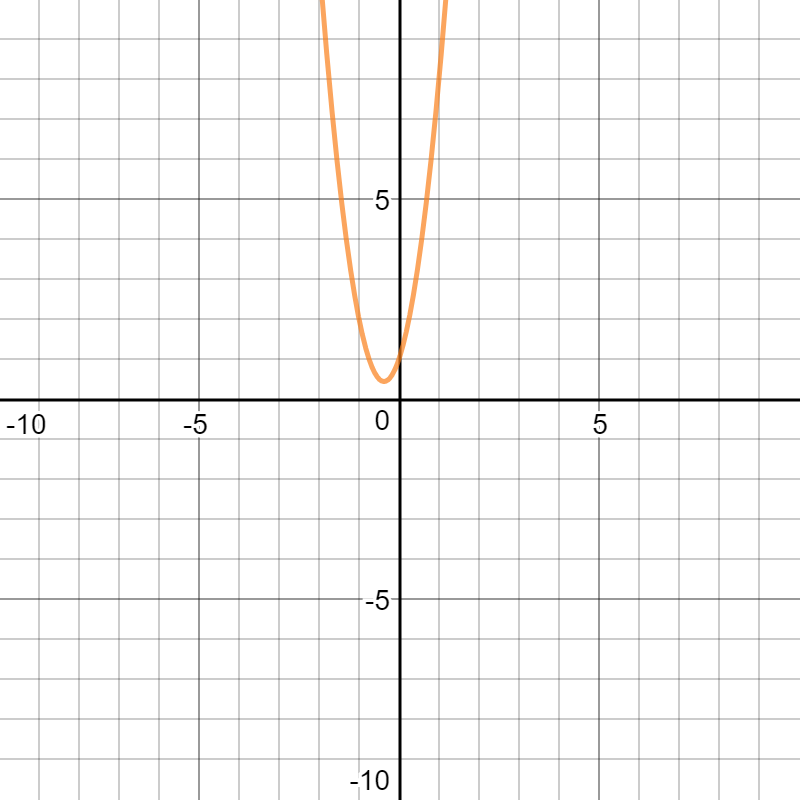
Finally, the correct answer Selection A
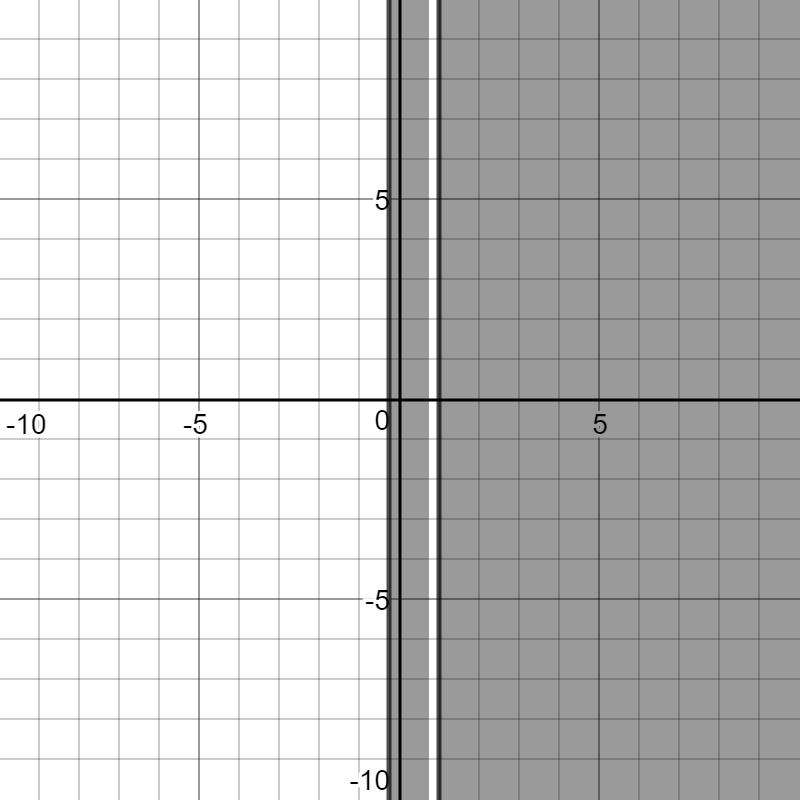
Please observe that the graph of the original inequality is identical to this graph with the same domain,


