What is the arc length of a semicircle if the diameter is 10?
Please help me with this! I have tried and tried and just couldn't get the answer! PLEASE HELP ME!!! DX
Please help me with this! I have tried and tried and just couldn't get the answer! PLEASE HELP ME!!! DX
1 Answer
Mar 19, 2018
Explanation:
The arc length of a circle has it's own formula:
Since this is a
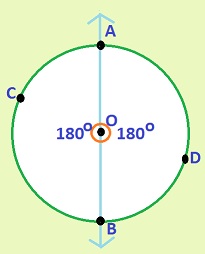
Use your calculator to find the value of
So the arc measure of the semi circle is

